
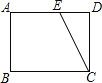
【题目】如图,在矩形纸片ABCD中,已知AB=6,BC=8,E是边AD上的点,以CE为折痕折叠纸片,使点D落在点F处,连接FC,当△AEF为直角三角形时,DE的长为________.
【答案】3或6.
【解析】
如图1,所示,由∠CFE+∠AFE=180°,可知点A、F、C在一条直线上,先求得AC的长,然后由△AEF∽△ACD可求得ED的长;如图2所示,可证明四边形CDEF为正方形从而可求得ED的长.
如图1所示:
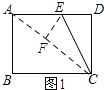
由翻折的性质可知:EF=ED,∠EFC=∠EDC=90°,
∵△AEF为直角△,
∴∠AFE=90°.
∴∠CFE+∠AFE=180°.
∴点A、F、C在一条直线上.
在Rt△ABC中,AC=![]() .
.
设DE=x,则EF=x.
∵∠EAF=∠DAC,∠EFA=∠CDA,
∴△AEF∽△ACD.
∴![]() ,即
,即![]() .
.
解得:x=3.
∴ED=3.
如图2所示:
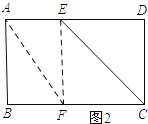
∵∠AEF=90°,
∴∠FED=90°.
∴∠FED=∠D=∠DCF=90°.
∴四边形CDEF为矩形.
由翻折的性质可知:DE=EF.
∴四边形CDEF为正方形.
∴DE=DC=6.
综上所述,ED的长为3或6.
故答案为:3或6.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】“国美”、“苏宁”两家电器商场出售同样的空气净化器和过滤网,空气净化器和过滤网在两家商场的售价一样.已知买一个空气净化器和![]() 个过滤网要花费
个过滤网要花费![]() 元,买
元,买![]() 个空气净化器和
个空气净化器和![]() 个过滤网要花费
个过滤网要花费![]() 元.
元.
(![]() )请用方程组求出一个空气净化器与一个过滤网的销售价格分别是多少元?
)请用方程组求出一个空气净化器与一个过滤网的销售价格分别是多少元?
(![]() )为了迎接新年,两家商场都在搞促销活动,“国美”规定:这两种商品都打九五折;“苏宁”规定:买一个空气净化器赠送两个过滤网.若某单位想要买
)为了迎接新年,两家商场都在搞促销活动,“国美”规定:这两种商品都打九五折;“苏宁”规定:买一个空气净化器赠送两个过滤网.若某单位想要买![]() 个空气净化器和
个空气净化器和![]() 个过滤网,如果只能在一家商场购买,请问选择哪家商场购买更合算?请说明理由.
个过滤网,如果只能在一家商场购买,请问选择哪家商场购买更合算?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋里装有分别标有数字1,2,3,4四个小球,除数字不同外,小球没有任何区别,每次实验先搅拌均匀.
(1)若从中任取一球,球上的数字为偶数的概率为多少?
(2)若从中任取一球(不放回),再从中任取一球,请用画树状图或列表格的方法求出两个球上的数字之和为偶数的概率.
(3)若设计一种游戏方案:从中任取两球,两个球上的数字之差的绝对值为1为甲胜,否则为乙胜,请问这种游戏方案设计对甲、乙双方公平吗?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△BDE中,∠BDE=90°,BD=6 ![]() ,点D的坐标是(7,0),∠BDO=15°,将△BDE旋转到△ABC的位置,点C在BD上,则旋转中心的坐标为 .
,点D的坐标是(7,0),∠BDO=15°,将△BDE旋转到△ABC的位置,点C在BD上,则旋转中心的坐标为 . 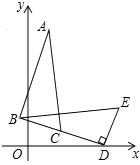
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,∠B=30°

(1)作边AB的垂直平分线交AB于点D,交BC于点E(尺规作图,不写作法,保留作图痕迹).
(2)连接AE,求证:AE=2DE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1和图2中的正方形ABCD和四边形AEFG都是正方形. 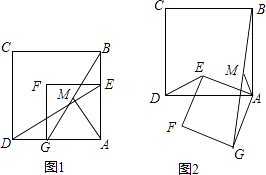
(1)如图1,连接DE,BG,M为线段BG的中点,连接AM,探究AM与DE的数量关系和位置关系,并证明你的结论;
(2)在图1的基础上,将正方形AEFG绕点A逆时针方向旋转到图2的位置,连结DE、BG,M为线段BG的中点,连结AM,探究AM与DE的数量关系和位置关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.
(1)当直线MN绕点C旋转到图1的位置时,求证:DE=AD+BE;
(2)当直线MN绕点C旋转到图2的位置时,求证:DE=AD-BE;
(3)当直线MN绕点C旋转到图3的位置时,试问DE、AD、BE具有怎样的等量关系?请直接写出这个等量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,直线l:y=x﹣1与x轴交于点A1 , 如图所示依次作正方形A1B1C1O、正方形A2B2C2C1、…、正方形AnBnCnCn﹣1 , 使得点A1、A2、A3、…在直线l上,点C1、C2、C3、…在y轴正半轴上,则点Bn的坐标是 . 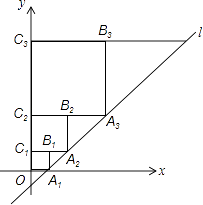
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com