
【题目】如图,△ABC的两条中线AD、CE交于点G,且AD⊥CE.连接BG并延长与AC交于点F,若AD=9,CE=12,则GF为 . 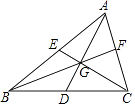
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
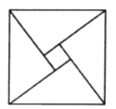
【题目】2002年8月在北京召开的国际数学家大会会标取材于我国古代数学家赵爽的《勾股圆方图》,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形(如图).如果大正方形的面积是100,小正方形的面积是4,直角三角形较短的直角边长为![]() ,较长的直角边长为
,较长的直角边长为![]() ,那么
,那么![]() 的值是_________.
的值是_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,P是对角线BD上一点,连接AP、![]() ,BF⊥AP于H,CP、BH延长线分别交AD边于点E、F。
,BF⊥AP于H,CP、BH延长线分别交AD边于点E、F。
(1)求证:∠DAP=∠DCE
(2)求证:AE=FD
(3)猜想∠APE与∠FBD的数量关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
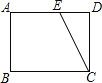
【题目】如图,在矩形纸片ABCD中,已知AB=6,BC=8,E是边AD上的点,以CE为折痕折叠纸片,使点D落在点F处,连接FC,当△AEF为直角三角形时,DE的长为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的顶点A(0,1),B(3,2),C(1,4)均在正方形网格的格点上.
(1)画出△ABC关于x轴对称的图形△A1B1C1;
(2)写出顶点A1,B1,C1的坐标;
(3)若正方形网格每两个格点间为一个单位长度,求△A1B1C1的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)某学习小组在探究三角形全等时,发现了下面这种典型的基本图形.如图①,已知:在△ABC中,∠BAC=90°,AB=AC,直线L经过点A,BD⊥直线L,CE⊥直线L,垂足分别为点D、E.证明:DE=BD+CE.
(2)组员小刘想,如果三个角不是直角,那结论是否会成立呢?如图②,将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线L上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
(3)数学老师赞赏了他们的探索精神,并鼓励他们运用这个知识来解决问题:如图③,过△ABC的边AB、AC向外作正方形ABDE和正方形ACFG,AH是BC边上的高,延长HA交EG于点I,求证:I是EG的中点.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平行四边形ABCD中,过点D作DE⊥AB于点E,点F在CD上,CF=AE,连接BF,AF. 
(1)求证:四边形BFDE是矩形;
(2)若AF平分∠BAD,且AE=3,DE=4,求矩形BFDE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=90°,AB=BC,BD⊥AC于点D;CE平分∠ACB,交AB于点E,交BD于点F.
(1)求证:△BEF是等腰三角形;
(2)求证:BD=![]() (BC+BF).
(BC+BF).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法:①![]() =﹣10;②数轴上的点与实数成一一对应关系;③一个数的算术平方根仍是它本身,这样的数有三个;④任何实数不是有理数就是无理数;⑤两个无理数的和还是无理数;⑥无理数都是无限小数,正确的个数有( )
=﹣10;②数轴上的点与实数成一一对应关系;③一个数的算术平方根仍是它本身,这样的数有三个;④任何实数不是有理数就是无理数;⑤两个无理数的和还是无理数;⑥无理数都是无限小数,正确的个数有( )
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com