
【题目】如图,在Rt△ABC中,∠C=90°,∠B=30°

(1)作边AB的垂直平分线交AB于点D,交BC于点E(尺规作图,不写作法,保留作图痕迹).
(2)连接AE,求证:AE=2DE.
【答案】(1)详见解析;(2)详见解析.
【解析】
试题(1)根据作线段垂直平分线方法作出图形即可;(2)在Rt△ABC中,∠C=90°,∠B=30°,根据直角三角形两锐角互余可得∠CAB=60°,由线段垂直平分线的性质可得AE=BE,即可得∠BAE=∠B=30°,所以∠CAE=60°﹣30°=30°,在Rt△ACE中,根据30°的锐角所对的直角边等于斜边的一半可得AE=2CE,再由角平分线的性质得出CE=DE即可得结论.
试题解析: 解:(1)如图所示;
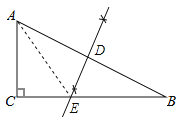
(2)∵在Rt△ABC中,∠C=90°,∠B=30°,
∴∠CAB=60°.
∵边AB的垂直平分线交AB于点D,交BC于点E,
∴AE=BE,
∴∠BAE=∠B=30°,
∴∠CAE=60°﹣30°=30°,
∴AE=2CE.
∵∠BAE=∠CAE=30°,
∴AE是∠BAC的平分线,
∴CE=DE,
∴AE=2DE.


科目:初中数学 来源: 题型:
【题目】《九章算术》是我国古代数学的经典著作,书中有一个问题:“今有黄金九枚,白银一十一枚,称之重适等.交易其一,金轻十三两.问金、银一枚各重几何?”.意思是:甲袋中装有黄金9枚(每枚黄金重量相同),乙袋中装有白银11枚(每枚白银重量相同),称重两袋相等.两袋互相交换1枚后,甲袋比乙袋轻了13两(袋子重量忽略不计).问黄金、白银每枚各重多少两?设每枚黄金重x两,每枚白银重y两,根据题意得( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,P是对角线BD上一点,连接AP、![]() ,BF⊥AP于H,CP、BH延长线分别交AD边于点E、F。
,BF⊥AP于H,CP、BH延长线分别交AD边于点E、F。
(1)求证:∠DAP=∠DCE
(2)求证:AE=FD
(3)猜想∠APE与∠FBD的数量关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
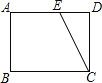
【题目】如图,在矩形纸片ABCD中,已知AB=6,BC=8,E是边AD上的点,以CE为折痕折叠纸片,使点D落在点F处,连接FC,当△AEF为直角三角形时,DE的长为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的顶点A(0,1),B(3,2),C(1,4)均在正方形网格的格点上.
(1)画出△ABC关于x轴对称的图形△A1B1C1;
(2)写出顶点A1,B1,C1的坐标;
(3)若正方形网格每两个格点间为一个单位长度,求△A1B1C1的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平行四边形ABCD中,过点D作DE⊥AB于点E,点F在CD上,CF=AE,连接BF,AF. 
(1)求证:四边形BFDE是矩形;
(2)若AF平分∠BAD,且AE=3,DE=4,求矩形BFDE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,已知△ABC≌△FDE,若A点的坐标为(a,1),BC∥x轴,B点的坐标为(b,-2),D、E两点都在y轴上,则F点到y轴的距离为_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com