
【题目】如图,PA与⊙O相切于点A,弦AB⊥OP,垂足为C,OP与⊙O相交于D点,已知OP=4,∠OPA=30°.求OC和AB的长. 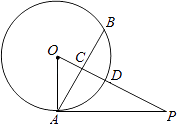
【答案】解:∵PA与⊙O相切于点A, ∴∠OAP=90°.
∵在Rt△OAP中,∠OPA=30°,
∴∠AOP=60°.
∵AB⊥OP,
∴∠OAC=30°,
∴ ![]() ,
, ![]() ,
,
∴ ![]() ,
,
∴ ![]() .
.
【解析】利用切线的性质和垂径定理推知△OAP和△OCA为直角三角形.利用“30度角所对的直角边等于斜边的一半”求得OA、OC的长度;然后在直角△OAC中,利用勾股定理可以求得AC的长度,则AB=2AC.
【考点精析】本题主要考查了勾股定理的概念和切线的性质定理的相关知识点,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】如图,已知AB=AD,那么添加下列一个条件后,能判定△ABC≌△ADC的是( )

A. AC=AC B. ∠BAC=∠DAC C. ∠BCA=∠DCA D. ∠B=∠D
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,与y轴交于点C,且OA=OC,则下列结论:①abc<0;② ![]() ;③ac﹣b+1=0;④OAOB=﹣
;③ac﹣b+1=0;④OAOB=﹣ ![]() .其中正确结论的序号是 .
.其中正确结论的序号是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,AB=8cm,对角线AC,BD相交于点O,点E,F分别从B,C两点同时出发,以1cm/s的速度沿BC,CD运动,到点C,D时停止运动,设运动时间为t(s),△OEF的面积为s(cm2),则s(cm2)与t(s)的函数关系可用图象表示为( )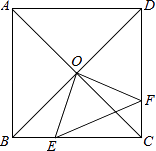
A.
B.
C.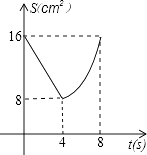
D.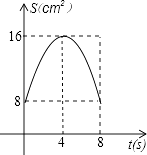
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,AB=AC=8cm,BC=6cm,D为AB中点,点P在AC上从C向A运动,运动速度为2(cm/s);同时,点Q在BC上从B向C运动,设点Q的运动速度为x(cm/s).且设P,Q的运动时间均为t秒,若其中一点先到达终点,则另一个点也将停止运动.

(1)如图2,当PD∥BC时,请解决下列问题:
①t= ;
②△ADP的形状为 (按“边”分类);
③若此时恰好有△BDQ≌△CPQ,请求出点Q运动速度x的值;
(2)当PD与BC不平行时,也有△BDQ与△CPQ全等:
①请求出相应的t与x的值;
②若设∠A=α°,请直接写出相应的∠DQP的度数(用含α的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋里装有分别标有数字1,2,3,4四个小球,除数字不同外,小球没有任何区别,每次实验先搅拌均匀.
(1)若从中任取一球,球上的数字为偶数的概率为多少?
(2)若从中任取一球(不放回),再从中任取一球,请用画树状图或列表格的方法求出两个球上的数字之和为偶数的概率.
(3)若设计一种游戏方案:从中任取两球,两个球上的数字之差的绝对值为1为甲胜,否则为乙胜,请问这种游戏方案设计对甲、乙双方公平吗?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,∠B=30°

(1)作边AB的垂直平分线交AB于点D,交BC于点E(尺规作图,不写作法,保留作图痕迹).
(2)连接AE,求证:AE=2DE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
在数学课上,老师提出如下问题:
已知:如图,四边形ABCD是平行四边形;

求作:菱形AECF,使点E,F分别在BC,AD上.
小凯的作法如下:
(1)连接AC;
(2)作AC的垂直平分线EF分别交BC,AD于E,F.
(3)连接AE,CF
所以四边形AECF是菱形.

老师说:“小凯的作法正确”.
回答下列问题:
根据小凯的做法,小明将题目改编为一道证明题,请你帮助小明完成下列步骤:
(1)已知:在平行四边形ABCD中,点E、F分别在边BC、AD上, .(补全已知条件)
求证:四边形AECF是菱形.
(2)证明:(写出证明过程)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com