
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,与y轴交于点C,且OA=OC,则下列结论:①abc<0;② ![]() ;③ac﹣b+1=0;④OAOB=﹣
;③ac﹣b+1=0;④OAOB=﹣ ![]() .其中正确结论的序号是 .
.其中正确结论的序号是 . 
【答案】①③④
【解析】解:观察函数图象,发现: 开口向下a<0;与y轴交点在y轴正半轴c>0;对称轴在y轴右侧﹣ ![]() >0;顶点在x轴上方
>0;顶点在x轴上方 ![]() >0.
>0.
① a<0,c>0,﹣ ![]() >0,
>0,
∴b>0,
∴abc<0,①成立;
② ![]() >0,
>0,
∴ ![]() <0,②不成立;
<0,②不成立;
③∵OA=OC,
∴xA=﹣c,
将点A(﹣c,0)代入y=ax2+bx+c中,
得:ac2﹣bc+c=0,即ac﹣b+1=0,③成立;
④∵OA=﹣xA , OB=xB , xAxB= ![]() ,
,
∴OAOB=﹣ ![]() ,④成立.
,④成立.
综上可知:①③④成立.
故答案为:①③④.
观察函数图象,根据二次函数图象与系数的关系找出“a<0,c>0,﹣ ![]() >0”,再由顶点的纵坐标在x轴上方得出
>0”,再由顶点的纵坐标在x轴上方得出 ![]() >0.①由a<0,c>0,﹣
>0.①由a<0,c>0,﹣ ![]() >0即可得知该结论成立;②由顶点纵坐标大于0即可得出该结论不成立;③由OA=OC,可得出xA=﹣c,将点A(﹣c,0)代入二次函数解析式即可得出该结论成立;④结合根与系数的关系即可得出该结论成立.综上即可得出结论.
>0即可得知该结论成立;②由顶点纵坐标大于0即可得出该结论不成立;③由OA=OC,可得出xA=﹣c,将点A(﹣c,0)代入二次函数解析式即可得出该结论成立;④结合根与系数的关系即可得出该结论成立.综上即可得出结论.


 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案科目:初中数学 来源: 题型:
【题目】如图,除公共边![]() 外,根据下列括号内三角形全等的条件,在横线上添加适当的条件,使
外,根据下列括号内三角形全等的条件,在横线上添加适当的条件,使![]() 与
与![]() 全等:
全等:
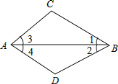
![]() ________,________
________,________![]() ;
;
![]() ________,________
________,________![]() ;
;
![]() ,________
,________![]() ;
;
![]() ________,
________,![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B,C,D在⊙O上,点O在∠D的内部,四边形OABC为平行四边形,则∠OAD+∠OCD=( ) 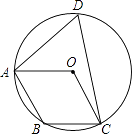
A.55°
B.60°
C.65°
D.70°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是我国古代数学的经典著作,书中有一个问题:“今有黄金九枚,白银一十一枚,称之重适等.交易其一,金轻十三两.问金、银一枚各重几何?”.意思是:甲袋中装有黄金9枚(每枚黄金重量相同),乙袋中装有白银11枚(每枚白银重量相同),称重两袋相等.两袋互相交换1枚后,甲袋比乙袋轻了13两(袋子重量忽略不计).问黄金、白银每枚各重多少两?设每枚黄金重x两,每枚白银重y两,根据题意得( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,
中,![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 与
与![]() 轴及直线
轴及直线![]() 分别交于点
分别交于点![]() .点
.点![]() 关于
关于![]() 轴对称,连接
轴对称,连接![]() .
.
(1)求点![]() 的坐标及直线
的坐标及直线![]() 的表达式;
的表达式;
(2)设面积的和![]() ,求
,求![]() 的值;
的值;
(3)在求(2)中![]() 时,嘉琪有个想法:“将
时,嘉琪有个想法:“将![]() 沿
沿![]() 轴翻折到
轴翻折到![]() 的位置,
的位置,![]() 与四边形
与四边形![]() 拼接后可看成
拼接后可看成![]() ,这样求
,这样求![]() 便转化为直接求
便转化为直接求![]() 的面积不更快捷吗?”但大家经反复验算,发现
的面积不更快捷吗?”但大家经反复验算,发现![]() ,请通过计算解释他的想法错在哪里.
,请通过计算解释他的想法错在哪里.

查看答案和解析>>
科目:初中数学 来源: 题型:
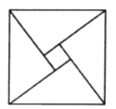
【题目】2002年8月在北京召开的国际数学家大会会标取材于我国古代数学家赵爽的《勾股圆方图》,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形(如图).如果大正方形的面积是100,小正方形的面积是4,直角三角形较短的直角边长为![]() ,较长的直角边长为
,较长的直角边长为![]() ,那么
,那么![]() 的值是_________.
的值是_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的顶点A(0,1),B(3,2),C(1,4)均在正方形网格的格点上.
(1)画出△ABC关于x轴对称的图形△A1B1C1;
(2)写出顶点A1,B1,C1的坐标;
(3)若正方形网格每两个格点间为一个单位长度,求△A1B1C1的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com