
【题目】如图,在平面直角坐标系![]() 中,
中,![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 与
与![]() 轴及直线
轴及直线![]() 分别交于点
分别交于点![]() .点
.点![]() 关于
关于![]() 轴对称,连接
轴对称,连接![]() .
.
(1)求点![]() 的坐标及直线
的坐标及直线![]() 的表达式;
的表达式;
(2)设面积的和![]() ,求
,求![]() 的值;
的值;
(3)在求(2)中![]() 时,嘉琪有个想法:“将
时,嘉琪有个想法:“将![]() 沿
沿![]() 轴翻折到
轴翻折到![]() 的位置,
的位置,![]() 与四边形
与四边形![]() 拼接后可看成
拼接后可看成![]() ,这样求
,这样求![]() 便转化为直接求
便转化为直接求![]() 的面积不更快捷吗?”但大家经反复验算,发现
的面积不更快捷吗?”但大家经反复验算,发现![]() ,请通过计算解释他的想法错在哪里.
,请通过计算解释他的想法错在哪里.

【答案】(1)C(-13,0),E(-5,-3),![]() ;(2)32;(3)见解析.
;(2)32;(3)见解析.
【解析】
(1)利用坐标轴上点的特点确定出点C的坐标,再利用直线的交点坐标的确定方法求出点E坐标,进而得到点B坐标,最后用待定系数法求出直线AB解析式;
(2)直接利用直角三角形的面积计算方法和直角梯形的面积的计算即可得出结论,
(3)先求出直线AB与x轴的交点坐标,判断出点C不在直线AB上,即可.
(1)在直线![]() 中,令y=0,则有0=
中,令y=0,则有0=![]() ,
,
∴x=﹣13,
∴C(﹣13,0),
令x=﹣5,代入![]() ,解得y=﹣3,
,解得y=﹣3,
∴E(﹣5,﹣3),
∵点B,E关于x轴对称,
∴B(﹣5,3),
∵A(0,5),
∴设直线AB的解析式为y=kx+5,
∴﹣5k+5=3,
∴k=![]() ,
,
∴直线AB的解析式为![]() ;
;
(2)由(1)知E(﹣5,﹣3),
∴DE=3,
∵C(﹣13,0),
∴CD=﹣5﹣(﹣13)=8,
∴S△CDE=![]() CD×DE=12,
CD×DE=12,
由题意知,OA=5,OD=5,BD=3,
∴S四边形ABDO=![]() (BD+OA)×OD=20,
(BD+OA)×OD=20,
∴S=S△CDE+S四边形ABDO=12+20=32;
(3)由(2)知,S=32,
在△AOC中,OA=5,OC=13,
∴S△AOC=![]() OA×OC=
OA×OC=![]() =32.5,
=32.5,
∴S≠S△AOC,
理由:由(1)知,直线AB的解析式为![]() ,令y=0,则0=
,令y=0,则0=![]() ,
,
∴x=﹣![]() ≠﹣13,
≠﹣13,
∴点C不在直线AB上,
即:点A,B,C不在同一条直线上,
∴S△AOC≠S.


科目:初中数学 来源: 题型:
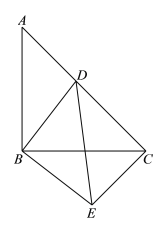
【题目】如图,△ABC和△DBE都是等腰直角三角形,点D在AC上,其中∠ABC=∠DBE=90°.
(1)求∠DCE的度数;
(2)当AB=5,AD:DC=2:3时,求DE的大小;
(3)当点D在线段AC上运动时(D不与A重合),请写出一个反映DA2,DC2,DB2之间关系的等式,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD纸片中,已知∠A=160°,∠B=30°,∠C=60°,四边形ABCD纸片分别沿EF,GH,OP,MN折叠,使A与A′、B与B′、C与C′、D与D′重合,则∠1+∠2+∠3+∠4+∠5+∠6+∠7﹣∠8的值是( )

A. 600° B. 700° C. 720° D. 800°
查看答案和解析>>
科目:初中数学 来源: 题型:
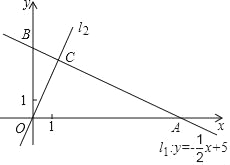
【题目】如图,直角坐标系xOy中,一次函数y=﹣![]() x+5的图象l1分别与x,y轴交于A,B两点,正比例函数的图象l2与l1交于点C(m,4).
x+5的图象l1分别与x,y轴交于A,B两点,正比例函数的图象l2与l1交于点C(m,4).
(1)求m的值及l2的解析式;
(2)求S△AOC﹣S△BOC的值;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,与y轴交于点C,且OA=OC,则下列结论:①abc<0;② ![]() ;③ac﹣b+1=0;④OAOB=﹣
;③ac﹣b+1=0;④OAOB=﹣ ![]() .其中正确结论的序号是 .
.其中正确结论的序号是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC中,点D , E , F分别是边AB , AC , BC上的点,DE∥BC , EF∥AB , 且AD:DB=4:7,那么CF:CB等于( ) 
A.7:11
B.4:8
C.4:7
D.3:7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,AB=AC=8cm,BC=6cm,D为AB中点,点P在AC上从C向A运动,运动速度为2(cm/s);同时,点Q在BC上从B向C运动,设点Q的运动速度为x(cm/s).且设P,Q的运动时间均为t秒,若其中一点先到达终点,则另一个点也将停止运动.

(1)如图2,当PD∥BC时,请解决下列问题:
①t= ;
②△ADP的形状为 (按“边”分类);
③若此时恰好有△BDQ≌△CPQ,请求出点Q运动速度x的值;
(2)当PD与BC不平行时,也有△BDQ与△CPQ全等:
①请求出相应的t与x的值;
②若设∠A=α°,请直接写出相应的∠DQP的度数(用含α的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某建筑工程队利用一面墙(墙的长度不限),用40米长的篱笆围成一个长方形的仓库. 
(1)求长方形的面积是150平方米,求出长方形两邻边的长;
(2)能否围成面积220平方米的长方形?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com