
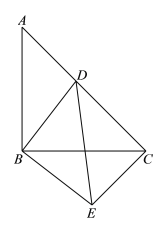
【题目】如图,△ABC和△DBE都是等腰直角三角形,点D在AC上,其中∠ABC=∠DBE=90°.
(1)求∠DCE的度数;
(2)当AB=5,AD:DC=2:3时,求DE的大小;
(3)当点D在线段AC上运动时(D不与A重合),请写出一个反映DA2,DC2,DB2之间关系的等式,并加以证明.
【答案】(1)∠DCE=90°;(2)![]() ;(3)2BD2=DA2+DC2,证明见解析.
;(3)2BD2=DA2+DC2,证明见解析.
【解析】
(1)由已知条件不难证明△ABD≌△CBE,可得∠A=∠ACB=∠BCE=45°,所以∠DCE=90°;(2)由AB=5可得AC=5![]() ,由AD:DC=2:3可以分别求出AD、CD的长度,进而求出CE的长度,利用勾股定理求出DE的长度即可;(3)由△BDE是等腰直角三角形,可得DE=
,由AD:DC=2:3可以分别求出AD、CD的长度,进而求出CE的长度,利用勾股定理求出DE的长度即可;(3)由△BDE是等腰直角三角形,可得DE=![]() BD,因为AD=CE,所以DE2=DC2+CE2=AD2+CD2,所以2BD2=AD2+CD2.
BD,因为AD=CE,所以DE2=DC2+CE2=AD2+CD2,所以2BD2=AD2+CD2.
(1)∵等腰直角△ABC,
∴AB=AC,∠ABC=90°,∠A=∠ACB=45°,
同理可得:DE=BE,∠DBE=90°,∠BDE=∠BED=45°,
∴∠ABD=∠CBE,
∵在△ABD与△CBE中,
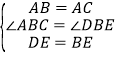 ,
,
∴△ABD≌△CBE,
∴∠A=∠ACB=∠BCE=45°,∠ABD=∠CBE,AD=CE,
∴∠DCE=90°;
(2)当AB=5,AD:DC=2:3时,有AC=![]() ,AD=
,AD=![]() ,DC=
,DC=![]() ,
,
在Rt△DCE中,CD=![]() ,CE=AD=
,CE=AD=![]() ,由勾股定理可得DE=
,由勾股定理可得DE=![]() ;
;
(3)2BD2=DA2+DC2;
∵△BDE是等腰直角三角形,
∴DE=![]() BD,
BD,
∵AD=CE,
∴DE2=DC2+CE2=AD2+CD2,
故2BD2=AD2+CD2.


科目:初中数学 来源: 题型:
【题目】如图,已知二次函数图象的顶点在原点,直线y= ![]() x+4的图象与该二次函数的图象交于点A(m,8),直线与x轴的交点为C,与y轴的交点为B.
x+4的图象与该二次函数的图象交于点A(m,8),直线与x轴的交点为C,与y轴的交点为B.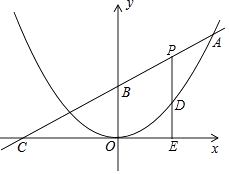
(1)求这个二次函数的解析式与B点坐标;
(2)P为线段AB上的一个动点(点P与A,B不重合),过P作x轴的垂线与这个二次函数的图象的交于点D,与x轴交于点E,设线段PD长为h,点P的横坐标为t,求h与t之间的函数关系式,并写出自变量t的取值范围;
(3)在(2)的条件下,在线段AB上是否存在点P.使得以点P,E,B为顶点的三角形为等腰三角形?若存在,请直接写P点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,AB是⊙O的直径,CE平分∠ACB交⊙O于点E,∠E=30°,交AB于点D,连接AE,则SADC:S△ADE的比值为( ) 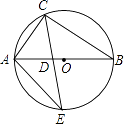
A.![]()
B.![]()
C.![]()
D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠BAC=90°,AB=AC=2cm,线段BC上一动点P从C点开始运动,到B点停止,以AP为边在AC的右侧作等边△APQ,则Q点运动的路径为cm. 
查看答案和解析>>
科目:初中数学 来源: 题型:
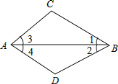
【题目】如图,除公共边![]() 外,根据下列括号内三角形全等的条件,在横线上添加适当的条件,使
外,根据下列括号内三角形全等的条件,在横线上添加适当的条件,使![]() 与
与![]() 全等:
全等:
![]() ________,________
________,________![]() ;
;
![]() ________,________
________,________![]() ;
;
![]() ,________
,________![]() ;
;
![]() ________,
________,![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
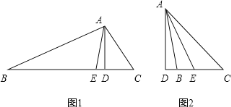
【题目】如图![]() ,在
,在![]() 中,
中,![]() 为
为![]() 边上的高,
边上的高,![]() 为
为![]() 的平分线,已知
的平分线,已知![]() ,
,![]()
![]() 求
求![]() 的度数;
的度数;
![]() 你发现
你发现![]() 与
与![]() 、
、![]() 之间有何关系?
之间有何关系?
![]() 若将“题中的条件
若将“题中的条件![]() ”改为“
”改为“![]() ”如图
”如图![]() ,其它条件不变,则
,其它条件不变,则![]() 与
与![]() 、
、![]() 之间又有何关系?请说明理由.
之间又有何关系?请说明理由.
![]() 若将“题目中的条件
若将“题目中的条件![]() ,
,![]() ”改为“
”改为“![]() ,
,![]() ”,其它条件不变,求
”,其它条件不变,求![]() 、
、![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了美化环境,学校准备在如图所示的矩形ABCD空地上进行绿化,规划在中间的一块四边形MNQP上种花,其余的四块三角形上铺设草坪,要求AM=AN=CP=CQ,已知BC=24米,AB=40米,设AN=x米,种花的面积为y1平方米,草坪面积y2平方米. 
(1)分别求y1和y2与x之间的函数关系式(不要求写出自变量的取值范围);
(2)当AN的长为多少米时,种花的面积为440平方米?
(3)若种花每平方米需200元,铺设草坪每平方米需100元,现设计要求种花的面积不大于440平方米,设学校所需费用W(元),求W与x之间的函数关系式,并求出学校所需费用的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,
中,![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 与
与![]() 轴及直线
轴及直线![]() 分别交于点
分别交于点![]() .点
.点![]() 关于
关于![]() 轴对称,连接
轴对称,连接![]() .
.
(1)求点![]() 的坐标及直线
的坐标及直线![]() 的表达式;
的表达式;
(2)设面积的和![]() ,求
,求![]() 的值;
的值;
(3)在求(2)中![]() 时,嘉琪有个想法:“将
时,嘉琪有个想法:“将![]() 沿
沿![]() 轴翻折到
轴翻折到![]() 的位置,
的位置,![]() 与四边形
与四边形![]() 拼接后可看成
拼接后可看成![]() ,这样求
,这样求![]() 便转化为直接求
便转化为直接求![]() 的面积不更快捷吗?”但大家经反复验算,发现
的面积不更快捷吗?”但大家经反复验算,发现![]() ,请通过计算解释他的想法错在哪里.
,请通过计算解释他的想法错在哪里.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com