
����Ŀ����ͼ����֪���κ���ͼ��Ķ�����ԭ�㣬ֱ��y= ![]() x+4��ͼ����ö��κ�����ͼ���ڵ�A��m��8����ֱ����x��Ľ���ΪC����y��Ľ���ΪB��
x+4��ͼ����ö��κ�����ͼ���ڵ�A��m��8����ֱ����x��Ľ���ΪC����y��Ľ���ΪB��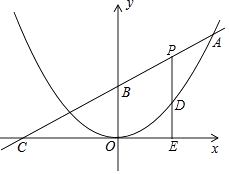
��1����������κ����Ľ���ʽ��B�����ꣻ
��2��PΪ�߶�AB�ϵ�һ�����㣨��P��A��B���غϣ�����P��x��Ĵ�����������κ�����ͼ��Ľ��ڵ�D����x�ύ�ڵ�E�����߶�PD��Ϊh����P�ĺ�����Ϊt����h��t֮��ĺ�����ϵʽ����д���Ա���t��ȡֵ��Χ��
��3���ڣ�2���������£����߶�AB���Ƿ���ڵ�P��ʹ���Ե�P��E��BΪ�����������Ϊ���������Σ������ڣ���ֱ��дP�����ꣻ�������ڣ���˵�����ɣ�
���𰸡�
��1��
�⣺�ߵ�A��m��8����ֱ��y= ![]() x+4�ϣ�
x+4�ϣ�
�� ![]() m+4=8�����m=8��
m+4=8�����m=8��
��A��8��8����
�������߹�ԭ�㣬
�������κ����Ľ���ʽΪy=ax2��a��0����
��A��8��8����y=ax2ͼ���ϣ�
��8=a��82�����a= ![]() ��
��
����κ����Ľ���ʽΪy= ![]() x2��
x2��
��ֱ��y=x+4��y�ύ�ڵ�B��
����x=0ʱ�ɵ�y=4����B��0��4��
��2��
�⣺��P����y= ![]() x+4�ϣ��Һ�����Ϊt��
x+4�ϣ��Һ�����Ϊt��
��P��t�� ![]() t+4����
t+4����
��PD��X����E��
��D��t�� ![]() ����E��t��0����
����E��t��0����
��PD=h=PE��DE=�� ![]() t+4����
t+4���� ![]() ��
��
��h=�� ![]() +
+ ![]() t+4��
t+4��
��P��A��B���غ������߶��ϣ�
��0��t��8��
��h��t�ĺ�����ϵʽΪh=�� ![]() +
+ ![]() t+4��0��t��8��
t+4��0��t��8��
��3��
�⣺��E��n��0����0��n��8������P��n�� ![]() n+4������B��0��4����
n+4������B��0��4����
��PB= ![]() =
= ![]() n��PE=
n��PE= ![]() n+4��BE=
n+4��BE= ![]() =
= ![]() ��
��
����PEB��������������PB=PE��PB=BE��PE=BE���������
�� ��PB=PEʱ������ ![]() n=
n= ![]() n+4�����n=2
n+4�����n=2 ![]() +2����ʱP������Ϊ��2
+2����ʱP������Ϊ��2 ![]() +2��
+2�� ![]() +5����
+5����
�ڵ�PB=BEʱ������ ![]() n=
n= ![]() �����n=8����ʱP��A�غϣ��������⣬��ȥ����n=��8��0��ȥ��
�����n=8����ʱP��A�غϣ��������⣬��ȥ����n=��8��0��ȥ��
�۵�PE=BEʱ������ ![]() n+4=
n+4= ![]() �����n=0����ȥ����n=
�����n=0����ȥ����n= ![]() ����ʱP������Ϊ��
����ʱP������Ϊ�� ![]() ��
�� ![]() ����
����
���Ͽ�֪��������������P�㣬������Ϊ��2 ![]() +2��
+2�� ![]() +5����
+5���� ![]() ��
�� ![]() ��
��
����������1����A���������ֱ�߽���ʽ�������m��ֵ�������A�����꣬���ô���ϵ��������������߽���ʽ�����ֱ�߽���ʽ�����B�����ꣻ��2����ֱ�ߺ������߽���ʽ�ɷֱ���t��ʾ��P��D�����꣬��ɱ�ʾ��PD�ij������ҵ�h��t�Ĺ�ϵʽ���ɵ�P���߶�AB�Ͽ�ȷ����t��ȡֵ��Χ����3������E������Ϊ��n��0���������n��ʾ��P�����꣬�Ӷ��ɱ�ʾ��PB��PE��BE�ij��ȣ�����PEBΪ����������ʱ������PB=PE��PB=BE��PE=BE����������ֱ�ɵõ�����n�ķ��̣������n��ֵ��������P�����꣮
�����㾫�����������⣬������Ҫ�˽���κ�����ͼ��(���κ���ͼ��ؼ��㣺1�����ڷ���2���Գ��� 3������ 4����x�ύ�� 5����y�ύ��)����Ҫ���ն��κ���������(�����ԣ���a>0ʱ���Գ�����ߣ�y��x�������С���Գ����ұߣ�y��x���������a<0ʱ���Գ�����ߣ�y��x��������Գ����ұߣ�y��x�������С)�����֪ʶ���Ǵ���Ĺؼ���


 ����������ϵ�д�
����������ϵ�д� �Ż���ҵ�Ϻ��Ƽ����׳�����ϵ�д�
�Ż���ҵ�Ϻ��Ƽ����׳�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,��5��5��������������,ÿ��С�����εı߳�����1,�����������а�����Ҫ��ͼ��:

��1����֪��A�ڸ��(��С�����εĶ���)��,��һ���߶�AB,����Ϊ![]() ,�ҵ�B�ڸ����;
,�ҵ�B�ڸ����;
��2���������������߶�ABΪһ��,���������߳��ֱ���3,![]() ,��һ��������ABC,ʹ��C�ڸ����(ֻ�軭������������һ��������);
,��һ��������ABC,ʹ��C�ڸ����(ֻ�軭������������һ��������);
��3��������������ABC��AB���ϸ��߳�Ϊ_________(ֱ��д����)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У���ͼ����֪Rt��DOE����DOE=90�㣬OD=3����D��y���ϣ���E��x���ϣ��ڡ�ABC�У���A��C��x���ϣ�AC=5����ACB+��ODE=180�㣬��ABC=��OED��BC=DE��������Ҫ��ͼ��������ͼ�ۼ�����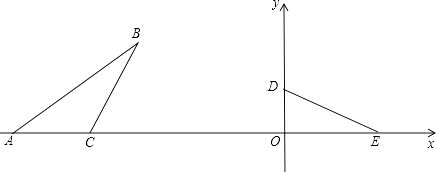
��1������ODE��O�㰴��ʱ�뷽����ת90��õ���OMN�����е�D�Ķ�Ӧ��Ϊ��M����E�Ķ�Ӧ��Ϊ��N����������OMN��
��2������ABC��x������ƽ�Ƶõ���A��B��C�䣨���е�A��B��C�Ķ�Ӧ��ֱ�Ϊ��A�䣬B�䣬C�䣩��ʹ��B��C���루1���еġ�OMN�ı�NM�غϣ�
��3����OE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������⣺
��1����֪һԪ���η���ax2+bx+c=0��a��0��������x1 �� x2��b2��4ac��0�����������ʽд��x1 �� x2 �� ��֤��x1+x2=�� ![]() ��x1x 2=
��x1x 2= ![]()
��2����һԪ���η���x2+x��1=0������Ϊm��n�����ã�1���еĽ��ۣ��� ![]() +
+ ![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��MON=30�㣬��A1��A2��A3����������ON�ϣ���B1��B2��B3����������OM�ϣ���A1B1A2����A2B2A3����A3B3A4������Ϊ�ȱ������Σ���OA2=4�����AnBnAn+1�ı߳�Ϊ__________��
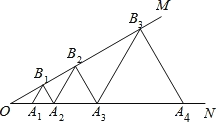
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�����ABO�Ƶ�A˳ʱ����ת����AB1C1��λ�ã���B��O�ֱ����ڵ�B1��C1������B1��x���ϣ��ٽ���AB1C1�Ƶ�B1˳ʱ����ת����A1B1C2��λ�ã���C2��x���ϣ�����A1B1C2�Ƶ�C2˳ʱ����ת����A2B2C2��λ�ã���A2��x���ϣ����ν�����ȥ��������A��3��0����B��0��4�������B100������Ϊ �� 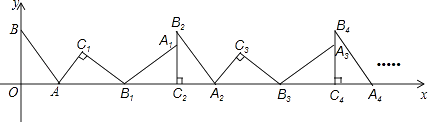
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���۲����µ�ʽ��
��1����ʽ��![]() +
+![]() +
+![]() ��
��![]() =1��
=1��
��2����ʽ��![]() +
+![]() +
+![]() ��
��![]() =1��
=1��
��3����ʽ��![]() +
+![]() +
+![]() ��
��![]() =1��
=1��
��4����ʽ��![]() +
+![]() +
+![]() ��
��![]() =1��
=1��
��5����ʽ��![]() +
+![]() +
+![]() ��
��![]() =1��
=1��
����
�������Ϲ��ɣ�����������⣺
��1��д����6����ʽ��_____��
��2��д�������ĵ�n����ʽ��_____���ú�n�ĵ�ʽ��ʾ������֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
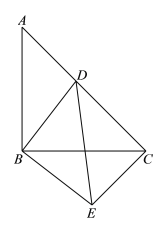
����Ŀ����ͼ����ABC�͡�DBE���ǵ���ֱ�������Σ���D��AC�ϣ����С�ABC=��DBE=90��.
(1)���DCE�Ķ�����
(2)��AB=5��AD��DC=2��3ʱ����DE�Ĵ�С��
(3)����D���߶�AC���˶�ʱ(D����A�غ�)����д��һ����ӳDA2��DC2��DB2֮���ϵ�ĵ�ʽ��������֤��.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com