
【题目】阅读下面材料:
在数学课上,老师提出如下问题:
已知:如图,四边形ABCD是平行四边形;

求作:菱形AECF,使点E,F分别在BC,AD上.
小凯的作法如下:
(1)连接AC;
(2)作AC的垂直平分线EF分别交BC,AD于E,F.
(3)连接AE,CF
所以四边形AECF是菱形.

老师说:“小凯的作法正确”.
回答下列问题:
根据小凯的做法,小明将题目改编为一道证明题,请你帮助小明完成下列步骤:
(1)已知:在平行四边形ABCD中,点E、F分别在边BC、AD上, .(补全已知条件)
求证:四边形AECF是菱形.
(2)证明:(写出证明过程)
【答案】(1)EF垂直平分AC;(2)证明见解析
【解析】
(1)根据菱形对角线互相垂直且平分添加即可;(2)如图:根据垂直平分线的性质可证明AE=CE、AF=CF,再由ABCD是平行四边形可证明∠FAC=∠ECA、∠AFE=∠FEC,即可证明△AOF≌△COE,进而证明AF=CE,即可证明AE=EC=CF=FA,可证明四边形AECF是菱形.
(1)添加EF垂直平分AC;
(2)∵EF垂直平分AC,
∴AF=CF,AE=EC,AO=CO,
∵AF//CE,
∴∠FAC=∠ECA、∠AFE=∠FEC,
∵AO=CO,
∴△AOF≌△COE,
∴AF=CE,
∴AE=EC=CF=FA,
∴四边形AECF是菱形.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的顶点A(0,1),B(3,2),C(1,4)均在正方形网格的格点上.
(1)画出△ABC关于x轴对称的图形△A1B1C1;
(2)写出顶点A1,B1,C1的坐标;
(3)若正方形网格每两个格点间为一个单位长度,求△A1B1C1的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平行四边形ABCD中,过点D作DE⊥AB于点E,点F在CD上,CF=AE,连接BF,AF. 
(1)求证:四边形BFDE是矩形;
(2)若AF平分∠BAD,且AE=3,DE=4,求矩形BFDE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( )

A. 当AB=BC时,它是菱形 B. 当AC⊥BD时,它是菱形
C. 当∠ABC=90°时,它是矩形 D. 当AC=BD时,它是正方形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=90°,AB=BC,BD⊥AC于点D;CE平分∠ACB,交AB于点E,交BD于点F.
(1)求证:△BEF是等腰三角形;
(2)求证:BD=![]() (BC+BF).
(BC+BF).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,∠DAE=∠E,∠B=∠D.直线AD与BE平行吗?直线AB与DC平行吗?说明理由(请在下面的解答过程的空格内填空或在括号内填写理由).

解:直线AD与BE平行,直线AB与DC .
理由如下:
∵∠DAE=∠E,(已知)
∴ ∥ ,(内错角相等,两条直线平行)
∴∠D=∠DCE. (两条直线平行,内错角相等)
又∵∠B=∠D,(已知)
∴∠B= ,(等量代换)
∴ ∥ .(同位角相等,两条直线平行)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,已知△ABC≌△FDE,若A点的坐标为(a,1),BC∥x轴,B点的坐标为(b,-2),D、E两点都在y轴上,则F点到y轴的距离为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A是反比例函数y1= ![]() (x>0)图象上一点,过点A作x轴的平行线,交反比例函数y2=
(x>0)图象上一点,过点A作x轴的平行线,交反比例函数y2= ![]() (x>0)的图象于点B,连接OA、OB,若△OAB的面积为2,则k的值为 .
(x>0)的图象于点B,连接OA、OB,若△OAB的面积为2,则k的值为 . 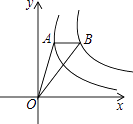
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com