
如图,是一张电脑光盘的表面,两个圆心都是O,大圆的弦AB所在的直线是小圆的切线,切点为C,已知大圆的半径为5cm,小圆的半径为1cm,则弦AB的长是 .

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2014-2015学年江苏省江阴市七年级上学期期中考试数学试卷(解析版) 题型:填空题
a※b是新规定的一种运算法则:a※b=a2+2ab-1,若(-2)※3=x,则x= .
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省江阴市华士片九年级上学期期中考试数学试卷(解析版) 题型:解答题
(本题12分)如图,在平面直角坐标系中,矩形OABC的两边OA、OC分别在x轴、y轴的正半轴上,OA=4,OC=2.点P从点O出发,沿x轴以每秒1个单位长的速度向点A匀速运动,当点P到达点A时停止运动,设点P运动的时间是t秒.将线段CP的中点绕点P按顺时针方向旋转90°得点D,点D随点P的运动而运动,连接DP、DA.


(1)请用含t的代数式表示出点D的坐标;
(2)求t为何值时,△DPA的面积最大,最大为多少?
(3)在点P从O向A运动的过程中,△DPA能否成为直角三角形?若能,求t的值.若不能,请说明理由;
(4)请直接写出随着点P的运动,点D运动路线的长.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省江阴市华士片九年级上学期期中考试数学试卷(解析版) 题型:解答题
(本题6分)已知:如图,在△ABC中,∠ACB=90°,∠B=25°,以点C为圆心.AC为半径作⊙C,交AB于点D,求 的度数.
的度数.

查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省江阴市华士片九年级上学期期中考试数学试卷(解析版) 题型:选择题
一件商品的原价是100元,经过两次提价后的价格为121元,如果每次提价的百分率都是x,根据题意,下面列出的方程正确的是( )
A.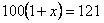 B.
B.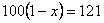
C. D.
D.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省八年级上学期期中联考数学试卷(解析版) 题型:解答题
(1)如图1,已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m, CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.
(2)如图2,将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC= ,其中
,其中 为任意锐角或钝角.请问结论“DE=BD+CE”是否成立?如成立,请你给出证明;若不成立,请说明理由.
为任意锐角或钝角.请问结论“DE=BD+CE”是否成立?如成立,请你给出证明;若不成立,请说明理由.
(3)如图3,D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com