
(1)如图1,已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m, CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.
(2)如图2,将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC= ,其中
,其中 为任意锐角或钝角.请问结论“DE=BD+CE”是否成立?如成立,请你给出证明;若不成立,请说明理由.
为任意锐角或钝角.请问结论“DE=BD+CE”是否成立?如成立,请你给出证明;若不成立,请说明理由.
(3)如图3,D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状.

(1)证明见试题解析;(2)成立,理由见试题解析;(3)等边三角形.
【解析】
试题分析:(1)由∠BDA=∠AEC=∠BAC=120°就可以求出∠BAD=∠ACE,进而由AAS就可以得出△BAD≌△ACE,就可以得出BD=AE,DA=CE而得出结论;
(2)由等边三角形的性质就可以求出∠BAC=120°,就可以得出△BAD≌△ACE,就有BD=AE,进而得出△BDF≌△AEF,得出DF=EF,∠BFD=∠AFE,而得出∠DFE=60°,就有△DEF为等边三角形.
试题解析:(1)DE=BD+CE成立.
理由:∵∠BDA=∠BAC=120°,∴∠DBA+∠DAB=∠CAE+∠DAB=60°,∴∠DBA=∠CAE.
在△BAD和△ACE中,∵∠BDA=∠AEC,∠DBA=∠CAE,BA=AC,∴△ADB≌△CEA(AAS),
∴AE=BD,AD=CE,∴DE=AE+AD=BD+CE;
(2)△DEF为等边三角形,理由:
∵△ABF和△ACF均为等边三角形,∴BF=AF=AB=AC=CF,∠BAF=∠CAF=∠ABF=60°,
∴∠BDA=∠AEC=∠BAC=120°,∴∠DBA+∠DAB=∠CAE+∠DAB=60°,∴∠DBA=∠CAE,
在△BAD和△ACE中,∵∠BDA=∠AEC,∠DBA=∠CAE,BA=AC,∴△ADB≌△CEA(AAS),
∴BD=AE,∠DBA=∠CAE.
∵∠ABF=∠CAF=60°,∴∠DBA+∠ABF=∠CAE+∠CAF,∴∠DBF=∠FAE.
在△BDF和△AEF中,∵FB=FA,∠DBF=∠FAE,BD=AE,∴△DBF≌△EAF(SAS)
∴DF=EF,∠BFD=∠AFE,∴∠DFE=∠DFA+∠AFE=∠DFA+∠BFD=60°,∴△DEF为等边三角形.
考点:1.全等三角形的判定与性质;2.等边三角形的判定与性质.


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:初中数学 来源:2014-2015学年江苏省江阴市华士片九年级上学期期中考试数学试卷(解析版) 题型:填空题
如图,是一张电脑光盘的表面,两个圆心都是O,大圆的弦AB所在的直线是小圆的切线,切点为C,已知大圆的半径为5cm,小圆的半径为1cm,则弦AB的长是 .

查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省江阴市华士片七年级上学期期中考试数学试卷(解析版) 题型:选择题
一潜水艇所在的海拔高度是?60米,一条海豚在潜水艇上方20米,则海豚所在的高度是海拔( )
A.?60米 B.?80米 C.?40米 D.40米
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省江都市九年级上学期期中考试数学试卷(解析版) 题型:选择题
已知关于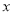 的一元二次方程
的一元二次方程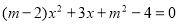 有一个解为
有一个解为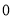 ,则
,则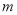 的值为( )
的值为( )
A.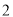 B.
B.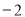 C.
C.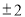 D.
D.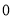
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省八年级上学期期中联考数学试卷(解析版) 题型:解答题
请在下列四个2×2的方格中,各画出一个三角形,要求所画三角形与图中三角形组成的图形是轴对称图形,且所画三角形顶点与方格中的小正方形顶点重合,并将所画三角形涂上阴影.(注:所画的四个图形不能重复)




查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省八年级上学期期中联考数学试卷(解析版) 题型:填空题
在高5米、长13米的一段台阶上铺上地毯,台阶的剖面图如图所示,则地毯的长度至少需要 米.

查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省七年级上学期期中联考数学试卷(解析版) 题型:解答题
出租车司机小王某天下午营运全是在东西走向的太湖大道上进行的.如果向东记作“+”,向西记作“-”.他这天下午行车情况如下:(单位:千米)
-2,+5,-1,+10,-3,-2,-5,+6
请回答:
(1)小王将最后一名乘客送到目的地时,小王在下午出车的出发地的什么方向?距下午出车的出发地多远?
(2)若规定每趟车的起步价是10元,且每趟车3千米以内(含3千米)只收起步价;若超过3千米,除收起步价外,超过的每千米还需收2元钱.那么小王这天下午共收到多少钱?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com