
(本题12分)如图,在平面直角坐标系中,矩形OABC的两边OA、OC分别在x轴、y轴的正半轴上,OA=4,OC=2.点P从点O出发,沿x轴以每秒1个单位长的速度向点A匀速运动,当点P到达点A时停止运动,设点P运动的时间是t秒.将线段CP的中点绕点P按顺时针方向旋转90°得点D,点D随点P的运动而运动,连接DP、DA.


(1)请用含t的代数式表示出点D的坐标;
(2)求t为何值时,△DPA的面积最大,最大为多少?
(3)在点P从O向A运动的过程中,△DPA能否成为直角三角形?若能,求t的值.若不能,请说明理由;
(4)请直接写出随着点P的运动,点D运动路线的长.
(1)点D(t+1, );(2)当t=2时,S最大=1;
);(2)当t=2时,S最大=1;
当t为2秒或3秒时,△DPA能成为直角三角形;
点D运动路线的长为 .
.
【解析】
试题分析:(1)设出P点坐标,再求出CP的中点坐标,根据相似的性质即可求出D点坐标;
(2)根据D点的坐标及三角形的面积公式直接求解即可;
(3)先判断出可能为直角的角,再根据勾股定理求解;
(4)根据点D的运动路线与OB平行且相等解答即可.
试题解析:(1)∵点P从点O出发,沿x轴以每秒1个单位长的速度向点A匀速运动,
∴OP=t,而OC=2,
∴P(t,0),
设CP的中点为F,
则F点的坐标为( ,1),
,1),
∴将线段CP的中点F绕点P按顺时针方向旋转90°得点D,其坐标为(t+1, );
);
(2)∵D点坐标为(t+1, ),OA=4,
),OA=4,
∴S△DPA= AP×
AP× =
= (4-t)×
(4-t)× =
= (4t-t2)=-
(4t-t2)=-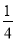 (t-2)2+1,
(t-2)2+1,
∴当t=2时,S最大=1;
(3)能构成直角三角形.
①当∠PDA=90°时,PC∥AD,
由勾股定理得, ,
,
即( )2+1+(4-t-1)2+(
)2+1+(4-t-1)2+( )2=(4-t)2,
)2=(4-t)2,
解得,t=2或t=-6(舍去).
∴t=2秒.
②当∠PAD=90°时,此时点D在AB上,
可知,△COP∽△PAD,
∴CP:PD=CO:PA,
∴2:1=2:PA,
PA=1,
即t+1=4,t=3秒.
综上,可知当t为2秒或3秒时,△DPA能成为直角三角形.
(4)∵根据点D的运动路线与OB平行且相等,OB= ,
,
∴点D运动路线的长为 .
.



考点:二次函数的最值;待定系数法求一次函数解析式;直角三角形的性质;矩形的性质.


科目:初中数学 来源:2014-2015学年江苏省江阴市八年级上学期期中考试数学试卷(解析版) 题型:填空题
如图,将一根25㎝长的细木棒放入长、宽、高分别为8㎝、6㎝和 ㎝的长方体无盖盒子中,则细木棒露在盒外面的最短长度是 ㎝.
㎝的长方体无盖盒子中,则细木棒露在盒外面的最短长度是 ㎝.

查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省江阴市九年级上学期期中考试数学试卷(解析版) 题型:选择题
用配方法解方程x2-2x-1=0时,配方后所得的方程为( )
A.(x+1) 2=0
B.(x-1) 2=0
C.(x+1) 2=2
D.(x-1) 2=2
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省江阴市七年级上学期期中考试数学试卷(解析版) 题型:填空题
江苏省的面积约为102600km2,这个数据用科学记数法可表示为 km2.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省江阴市七年级上学期期中考试数学试卷(解析版) 题型:选择题
把代数式“ ”用文字语言叙述,其中表述不正确的是( )
”用文字语言叙述,其中表述不正确的是( )
A.比x的倒数小5的数 B.x的倒数与5的差
C.x与5的差的倒数 D.1除以x的商与5的差
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省江阴市华士片九年级上学期期中考试数学试卷(解析版) 题型:解答题
(本题8分)如图,在4×3的正方形方格中,△ABC和△DEF的顶点都在边长为1的小正方形的顶点上.

(1)填空:∠ABC= °,BC= ;
(2)判断△ABC与△DEC是否相似,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省江阴市华士片九年级上学期期中考试数学试卷(解析版) 题型:填空题
如图,是一张电脑光盘的表面,两个圆心都是O,大圆的弦AB所在的直线是小圆的切线,切点为C,已知大圆的半径为5cm,小圆的半径为1cm,则弦AB的长是 .

查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省江阴市华士片七年级上学期期中考试数学试卷(解析版) 题型:解答题
(本题7分)
(1)当 ,
, 时,分别求代数式①
时,分别求代数式① ②
② 的值;
的值;
(2)当 ,
, 时,分别求代数式①
时,分别求代数式① ②
②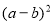 的值;
的值;
(3)观察(1)(2)中代数式的值, 与
与 有何关系?
有何关系?
(4)利用你发现的规律,求 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com