
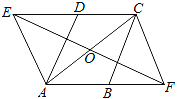
【题目】如图,在ABCD中,∠DAB=60°,点E、F分别在CD、AB的延长线上,且AE=AD,CF=CB.
(1)求证:四边形AFCE是平行四边形;
(2)若去掉已知条件的“∠DAB=60°”,上述的结论还成立吗?若成立,请写出证明过程;若不成立,请说明理由.
【答案】(1)见解析;(2)成立,见解析
【解析】试题分析:(1)由已知条件可得△AED,△CFB是正三角形,可得∠AEC=∠BFC=60°,∠EAF=∠FCE=120°,所以四边形AFCE是平行四边形.
(2)上述结论还成立,可以证明△ADE≌△CBF,可得∠AEC=∠BFC,∠EAF=∠FCE,所以四边形AFCE是平行四边形.
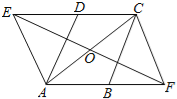
(1)证明:∵四边形ABCD是平行四边形,
∴DC∥AB,∠DCB=∠DAB=60°.
∴∠ADE=∠CBF=60°.
∵AE=AD,CF=CB,
∴△AED,△CFB是正三角形.
∴∠AEC=∠BFC=60°,∠EAF=∠FCE=120°.
∴四边形AFCE是平行四边形.
(2)解:上述结论还成立.
证明:∵四边形ABCD是平行四边形,
∴DC∥AB,∠CDA=∠CBA,∠DCB=∠DAB,AD=BC,DC=AB.
∴∠ADE=∠CBF.
∵AE=AD,CF=CB,
∴∠AED=∠ADE,∠CFB=∠CBF.
∴∠AED=∠CFB.
又∵AD=BC,
在△ADE和△CBF中.
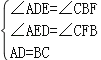 ,
,
∴△ADE≌△CBF(AAS).
∴∠AED=∠BFC,∠EAD=∠FCB.
又∵∠DAB=∠BCD,
∴∠EAF=∠FCE.
∴四边形EAFC是平行四边形.


科目:初中数学 来源: 题型:
【题目】将抛物线y=(x﹣1)2+1向下平移1个单位,所得新抛物线的解析式为( )
A.y=(x﹣1)2+2
B.y=(x﹣1)2
C.y=(x﹣2)2+1
D.y=x2+1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
点A、B在数轴上分别表示实数a、b,A、B两点之间的距离表示为∣AB∣.
当A、B两点中有一点在原点时,不妨设点A在原点,如图1,∣AB∣=∣OB∣=∣b∣=∣a-b∣;
![]()
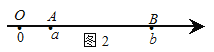
当A、B两点都不在原点时,如图2,点A、B都在原点的右边
∣AB∣=∣OB∣-∣OA∣=∣b∣-∣a∣=![]() =∣a-b∣;
=∣a-b∣;
如图3,当点A、B都在原点的左边,
∣AB∣=∣OB∣-∣OA∣=∣b∣-∣a∣=![]() =∣a-b∣;
=∣a-b∣;
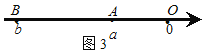
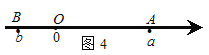
如图4,当点A、B在原点的两边,
∣AB∣=∣OB∣+∣OA∣=∣a∣+∣b∣= ![]() =∣a-b∣;
=∣a-b∣;
回答下列问题:
(1)数轴上表示1和6的两点之间的距离是 ,数轴上表示2和-3的两点之间的距离是 ;
(2)数轴上若点A表示的数是x,点B表示的数是-4,则点A和B之间的距离是 ,若∣AB∣=3,那么x为 ;
(3)当x是 时,代数式![]() ;
;
(4)若点A表示的数![]() ,点B与点A的距离是10,且点B在点A的右侧,动点P、Q同时从A、B出发沿数轴正方向运动,点P的速度是每秒3个单位长度,点Q的速度是每秒
,点B与点A的距离是10,且点B在点A的右侧,动点P、Q同时从A、B出发沿数轴正方向运动,点P的速度是每秒3个单位长度,点Q的速度是每秒![]() 个单位长度,求运动几秒后,点Q与点P 相距1个单位?(请写出必要的求解过程)
个单位长度,求运动几秒后,点Q与点P 相距1个单位?(请写出必要的求解过程)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com