
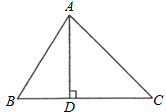
【题目】如图,在△ABC中,AD⊥BC,垂足为D,∠B=60°,∠C=45°,AC=![]() ,
,
(1)求AD的长. (2)求⊿ABC的面积。
【答案】(1)3;(2)![]()
【解析】试题分析:(1)根据三角形内角和可得∠DAC=45°,根据等角对等边可得AD=CD,然后再根据勾股定理可计算出AD的长;
(2)根据三角形内角和可得∠BAD=30°,再根据直角三角形的性质可得AB=2BD,然后利用勾股定理计算出BD的长,进而可得BC的长,然后利用三角形的面积公式计算即可.
试题解析:(1)∵∠C=45°,AD是△ABC的边BC上的高,
∴∠DAC=45°,
∴AD=CD,
∵AC2=AD2+CD2,
∴(![]() )2=2AD2,
)2=2AD2,
∴AD=3;
(2)在Rt△ADB中,∵∠B=60°,
∴∠BAD=30°,
∴AB=2BD,
∵AB2=BD2+AD2,
∴(2BD)2=BD2+AD2,
3BD2=9,
BD=![]() ,
,
∴△ABC的面积: ![]() BCAD=
BCAD=![]() (BD+DC)AD=
(BD+DC)AD=![]() ×(
×(![]() +3)×3=
+3)×3=![]() .
.


科目:初中数学 来源: 题型:
【题目】A、B、C、D、E、F六足球队进行单循环比赛,当比赛到某一天时,统计出A、B、C、D、E、五队已分别比赛了5、4、3、2、1场球,则还没与B队比赛的球队是
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过点A(﹣1,0)、B(3,0)的抛物线y=﹣x2+bx+c与y轴交于点C,它的对称轴与x轴交于点E.
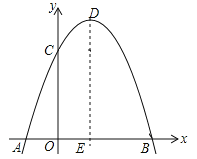
(1)求抛物线解析式;
(2)求抛物线顶点D的坐标;
(3)若抛物线的对称轴上存在点P使S△PCB=3S△POC,求此时DP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(﹣2,a),B(﹣1,b),C(3,c)均在抛物线y=﹣2(x+1)2+3上,则a,b,c的大小关系为( )
A. a<c<b B. b<a<c C. c<a<b D. a<b<c
查看答案和解析>>
科目:初中数学 来源: 题型:
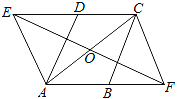
【题目】如图,在ABCD中,∠DAB=60°,点E、F分别在CD、AB的延长线上,且AE=AD,CF=CB.
(1)求证:四边形AFCE是平行四边形;
(2)若去掉已知条件的“∠DAB=60°”,上述的结论还成立吗?若成立,请写出证明过程;若不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将连续的偶数2,4,6,8……,排成如下表:

(1)十字框中的五个数的和与中间的数16有什么关系?
(2)设中间的数为x,用代数式表示十字框中的五个数的和,
(3)若将十字框上下左右移动,可框住另外的五个数,其它五个数的和能等于2010吗?如能,写出这五个数,如不能,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com