
【题目】如图,△ABC中,AB=AC,过点A作GE∥BC,角平分线BD、CF相交于点H,它们的延长线分别交GE于点E、G.试在图中找出3对全等三角形,并对其中一对全等三角形给出证明.

科目:初中数学 来源: 题型:
【题目】如图,直线AB,CD 相交于点O,∠AOD=3∠BOD+20°.
(1)求∠BOD的度数;
(2)以O为端点引射线OE,OF ,射线OE平分∠BOD,且∠EOF= 90°,求∠BOF的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校开展课外体育活动,决定开设A:篮球、B:乒乓球、C:踢毽子、D:跑步四种活动项目.为了解学生最喜欢哪一种活动项目(每人只选取一种),随机抽取了部分学生进行调查,并将调查结果绘成如甲、乙所示的统计图,请你结合图中信息解答下列问题. 
(1)样本中最喜欢A项目的人数所占的百分比为 , 其所在扇形统计图中对应的圆心角度数是度;
(2)请把条形统计图补充完整;
(3)若该校有学生1000人,请根据样本估计全校最喜欢踢毽子的学生人数约是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,一次函数y=k1x+6与x轴、y轴分别交于点A、B两点,与正比例函数y=k2x交于点D(2,2)
(1)求一次函数和正比例函数的表达式;
(2)若点P(m,m)为直线y=k2x上的一个动点(点P不与点D重合),点Q在一次函数y=k1x+6的图象上,PQ∥y轴,当PQ=![]() OA时,求m的值.
OA时,求m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△A1B1C1、△A2B2C2、△A3B3C3、…、△AnBnn均为等腰直角三角形,且∠C1=∠C2=∠C3=…=∠n=90°,点A1、A2、A3、…、An和点B1、B2、B3、…、Bn分别在正比例函数y=![]() x和y=﹣x的图象上,且点A1、A2、A3、…、An的横坐标分别为1,2,3…n,线段A1B1、A2B2、A3B3、…、AnBn均与y轴平行.按照图中所反映的规律,则△AnBnn的顶点n的坐标是_____;线段C2018C2019的长是_____.(其中n为正整数)
x和y=﹣x的图象上,且点A1、A2、A3、…、An的横坐标分别为1,2,3…n,线段A1B1、A2B2、A3B3、…、AnBn均与y轴平行.按照图中所反映的规律,则△AnBnn的顶点n的坐标是_____;线段C2018C2019的长是_____.(其中n为正整数)

查看答案和解析>>
科目:初中数学 来源: 题型:
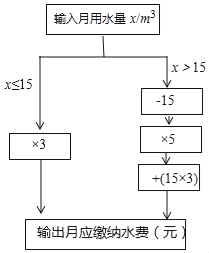
【题目】小明根据市自来水公司的居民用水收费标准,制定了水费计算数值转换机的示意图.(用水量单位:m3,水费单位:元)
(1)根据转换机程序计算下列各户月应缴纳水费
用户 | 张大爷 | 王阿姨 | 小明家 |
月用水量/m3 | 6 | 15 | 17 |
月应缴纳水费/元 |
|
|
|
(2)当x>15时,用含x的代数式表示水费 ;
(3)小丽家10月份水费是70元,小丽家10月份用水 m3.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的角平分线CD、BE相交于F,∠A=90°,EG∥BC,且CG⊥EG于G,下列结论:①∠CEG=2∠DCB;②∠ADC=∠GCD;③CA平分∠BCG;④∠DFB=![]() ∠CGE.其中正确的结论是( )
∠CGE.其中正确的结论是( )

A. ②③B. ①②④C. ①③④D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若一个两位正整数m的个位数为8,则称m为“好数”.
(1)求证:对任意“好数”m,m2-64一定为20的倍数;
(2)若m=p2-q2,且p,q为正整数,则称数对(p,q)为“友好数对”,规定: ![]() ,例如68=182-162,称数对(18,16)为“友好数对”,则
,例如68=182-162,称数对(18,16)为“友好数对”,则![]() ,求小于50的“好数”中,所有“友好数对”的H(m)的最大值.
,求小于50的“好数”中,所有“友好数对”的H(m)的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com