
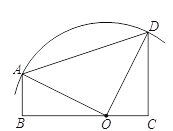
【题目】如图,梯形![]() 中,AB∥DC,AB⊥BC,AB=2cm,CD=4cm.以BC上一点O为圆心的圆经过A、D两点,且
中,AB∥DC,AB⊥BC,AB=2cm,CD=4cm.以BC上一点O为圆心的圆经过A、D两点,且![]() ,圆心O到弦AD的距离是____cm.
,圆心O到弦AD的距离是____cm.
【答案】![]() .
.
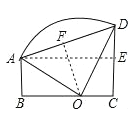
【解析】试题分析:如图,作AE⊥CD,垂足为E,OF⊥AD,垂足为F,
则四边形AECB是矩形,
CE=AB=2cm,DE=CD﹣CE=4﹣2=2cm,
∵∠AOD=90°,AO=OD,
所以△AOD是等腰直角三角形,
AO=OD,∠OAD=∠ADO=45°,BO=CD,
∵AB∥CD,
∴∠BAD+∠ADC=180°
∴∠ODC+∠OAB=90°,
∵∠ODC+∠DOC=90°,
∴∠DOC=∠BAO,
∵∠B=∠C=90°
∴△ABO≌△OCD,
∴OC=AB=2cm,OB=CD=4cm,BC=BO+OC=AE=6cm,
由勾股定理知,AD2=AE2+DE2,
得AD=2![]() cm,
cm,
∴AO=OD=2![]() cm,
cm,
S△AOD=![]() AODO=
AODO=![]() ADOF,
ADOF,
∴OF=![]() cm.
cm.


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点(﹣2,0),(x1,0),且1<x1<2,与y轴的正半轴的交点在(0,2)的下方,下列结论:①a<b<c;②2a+c>0;③4a+c<0;④2a﹣b+1>0.其中正确结论的个数为( )
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点B、E、C、F在一条直线上,AB=DF,AC=DE,∠A=∠D.
(1)求证:AC∥DE;
(2)若BF=13,EC=5,求BC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AD⊥EF,CE⊥EF,∠2+∠3=180°. 
(1)请你判断∠1与∠BDC的数量关系,并说明理由;
(2)若∠1=70°,DA平分∠BDC,试求∠FAB的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com