
��֪������y=Ax 2 +Bx+C��y�ύ�ڵ�A��0��3������x��ֱ���B��1��0����C��5��0������.
��1����������ߵĽ���ʽ��
��2������DΪ�߶�OA��һ�����ȷֵ㣬��ֱ��DC�Ľ���ʽ��
��3����һ������P��OA���е�M�������ȵ���x���ϵ�ij�㣨��Ϊ��E�����ٵ��������ߵĶԳ�����ij�㣨��Ϊ��F��������˶�����A.��ʹ��P�˶�����·����̵ĵ�E����F�����꣬�������������·���ij�.
��4������N������Ϊ��3��4����QΪx����һ�㣬��ONQΪ���������Σ���ֱ��д����Q�����ꡣ��14�֣�
��1�������ߵĽ���ʽΪ  ����2������D������Ϊ��0,1��ʱ��ֱ��CD�Ľ���ʽΪy=
����2������D������Ϊ��0,1��ʱ��ֱ��CD�Ľ���ʽΪy=  x+1; ����D������Ϊ��0,2��ʱ��ֱ��CD�Ľ���ʽΪy=
x+1; ����D������Ϊ��0,2��ʱ��ֱ��CD�Ľ���ʽΪy=  x+2.��3��
x+2.��3�� .��4��Q1��5,0��,Q2��-5,0��,Q3��
.��4��Q1��5,0��,Q2��-5,0��,Q3��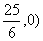 ,Q4��6,0��
,Q4��6,0��
��������
�����������1���������⣬C=3��
����
���
���������߽���ʽΪy= x2��
x2��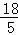 x+3��
x+3��
��2��������ɵ�OA�����ȷֵ�ֱ�Ϊ��0��1������0��2����
��ֱ��CD�Ľ���ʽΪy=kx+B��
����D������Ϊ��0��1��ʱ��ֱ��CD�Ľ���ʽΪy=�� x+1��
x+1��
����D������Ϊ��0��2��ʱ��ֱ��CD�Ľ���ʽΪy=�� x+2��
x+2��
��3����ͼ�������⣬�ɵ�M��0�� ����
����
�ߵ�M���M�����x��ĶԳƣ�
���ΪM�䣨0���� ����
����
���A���������߶Գ���x=3�ĶԳƵ�ΪA'��6��3����
����A'M'��
������Գ��Լ�������߶���̿�֪��A'M'�ij����������P�˶��������·���ij���
��A'M'��x��Ľ���Ϊ����E�㣬��ֱ��x=3�Ľ���Ϊ����F�㣮
������ֱ��A'M'�Ľ���ʽΪy= x��
x�� ��
��
��ɵ�E������Ϊ��2��0����F������Ϊ��3�� ����
����
�ɹ��ɶ�������� ��
��
���P�˶��������·����ME+EF+FA���ij�Ϊ ����8�֣�
����8�֣�

��4��Q1��5,0��,Q2��-5,0��,Q3��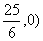 ,Q4��6,0��
,Q4��6,0��
���㣺���κ����ۺ�


 ��ʦ����ָ���ο�ʱϵ�д�
��ʦ����ָ���ο�ʱϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2014-2015ѧ�꽭��ʡ���꼶��ѧ�����п�����ѧ�Ծ��������棩 ���ͣ������
�Ƚϴ�С�� - ��-
��- ����-3 -
����-3 -
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ�꽭��ʡ�����а��꼶��ѧ�����п�����ѧ�Ծ��������棩 ���ͣ�ѡ����
�ڡ�ABC�У�AB=AC����C=75�㣬 ���A�Ķ����ǣ� ��
A��30�� B��50�� C��75�� D��150��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ�꽭��ʡ�����о��꼶��ѧ�����п�����ѧ�Ծ��������棩 ���ͣ������
��������y=x2����ƽ��1 ����λ��������ƽ��3����λ���õ������� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ�꽭��ʡ�����о��꼶��ѧ�����п�����ѧ�Ծ��������棩 ���ͣ�ѡ����
���κ���y=-2x2+1��ͼ����ͼ��ʾ������������ԭ��O��ת180�㣬����ת��������ߵĽ���ʽΪ�� ��
A��y=-2x2-1 B��y=2x2+1 C��y=2x2 D��y=2x2-1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ�꽭��ʡ�����о��꼶��ѧ�ڵ�һ�ε�Ԫ������ѧ�Ծ��������棩 ���ͣ������
��֪����ͼ��PΪ�ȱߡ�ABC��һ�㣬��APB=113�㣬��APC=123�㣬��˵������AP��BP��CPΪ�߳����Թ���һ�������Σ���ȷ�������������εĸ��ڽǵĶ�������8�֣�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ�꽭��ʡ�����о��꼶��ѧ�ڵ�һ�ε�Ԫ������ѧ�Ծ��������棩 ���ͣ������
����xȡ��ֵ�����κ���y=-x 2 +6x+C�ĺ���ֵ��Ϊ��������C��ȡֵ��ΧΪ____________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ�꽭��ʡ��ͨ�к����ذ��꼶��ѧ�����п�����ѧ�Ծ��������棩 ���ͣ������
��8�֣���ͼ��C���߶�BE��һ�㣬��BC��CEΪ�߷ֱ���BE��ͬ�����ȱߡ�ABC�͵ȱߡ�DCE������AE��BD.

��1����֤BD=AE��
��2����M��N�ֱ����߶�AE��BD�ϵĵ㣬��AM=BN�����жϡ�CMN����״����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ�꽭��ʡ��ͨ�а��꼶��ѧ�����п�����ѧ�Ծ��������棩 ���ͣ������
��ͼ����֪�ȱߡ�ABC�У�BD=CE��AD��BE�ཻ�ڵ�P�����APE�� ��.

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com