
【题目】定义:如图1,点M,N把线段AB分割成AM,MN和BN,若以AM,MN,BN为边的三角形是一个直角三角形,则称点M,N是线段AB的勾股分割点.
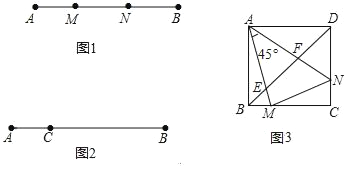
(1)已知点M,N是线段AB的勾股分割点,若AM=3,MN=4求BN的长;
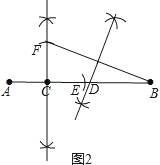
(2)已知点C是线段AB上的一定点,其位置如图2所示,请在BC上画一点D,使C,D是线段AB的勾股分割点(要求尺规作图,保留作图痕迹,画出一种情形即可);
(3)如图3,正方形ABCD中,M,N分别在BC,DC上,且BM≠DN,∠MAN=45°,AM,AN分别交BD于E,F.
求证:①E、F是线段BD的勾股分割点;
②△AMN的面积是△AEF面积的两倍.
【答案】(1)BN=![]() 或5;(2)图形见解析;(3)①证明见解析,②证明见解析.
或5;(2)图形见解析;(3)①证明见解析,②证明见解析.
【解析】试题分析:(1)①当MN为最大线段时,由勾股定理求出BN;由BN为最大线段时,由勾股定理求出BN即可;
(2)①在AB上截取CE=CA,②作AE的垂直平分线,并截取CF=CA,③连接BF,并作BF的垂直平分线,交AB于D;
(3)①如图3,将△ADF绕点A顺时针旋转90°得到△ABH,连接HE,只要证明△EAH≌△EAF,推出EF=HE,再证明∠HBE=90°即可;
②如图,连接FM,EN,证明△AEN和△AFM是等腰直角三角形,推出AM、AN,根据三角形的面积和锐角三角函数求解即可.
试题解析:(1)解:(1)①当MN为最大线段时,
∵点M,N是线段AB的勾股分割点,
∴BM=![]() =
=![]() =
=![]() ,
,
②当BN为最大线段时,
∵点M,N是线段AB的勾股分割点,
∴BN=![]() =
=![]() =5,
=5,
综上,BN=![]() 或5;
或5;
(2)作法:①在AB上截取CE=CA;
②作AE的垂直平分线,并截取CF=CA;
③连接BF,并作BF的垂直平分线,交AB于D;
点D即为所求;如图2所示.
(3)①如图3中,将△ADF绕点A顺时针性质90°得到△ABH,连接HE.
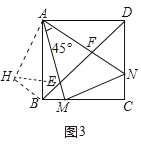
∵∠DAF+∠BAE=90°﹣∠EAF=45°,∠DAF=∠BAH,
∴∠EAH=∠EAF=45°,
∵EA=EA,AH=AF,
∴△EAH≌△EAF,
∴EF=HE,
∵∠ABH=∠ADF=45°=∠ABD,
∴∠HBE=90°,
在Rt△BHE中,HE2=BH2+BE2,
∵BH=DF,EF=HE,
∵EF2=BE2+DF2,
∴E、F是线段BD的勾股分割点.
②证明:如图4中,连接FM,EN.
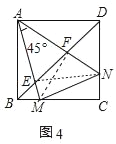
∵四边形ABCD是正方形,
∴∠ADC=90°,∠BDC=∠ADB=45°,
∵∠MAN=45°,
∴∠EAN=∠EDN,∵∠AFE=∠FDN,
∴△AFE∽△DFN,
∴∠AEF=∠DNF,![]() =
=![]() ,
,
∴![]() =
=![]() ,∵∠AFD=∠EFN,
,∵∠AFD=∠EFN,
∴△AFD∽△EFN,
∴∠DAF=∠FEN,
∵∠DAF+∠DNF=90°,
∴∠AEF+∠FEN=90°,
∴∠AEN=90°
∴△AEN是等腰直角三角形,
同理△AFM是等腰直角三角形;
∵△AEN是等腰直角三角形,同理△AFM是等腰直角三角形,
∴AM=![]() AF,AN=
AF,AN=![]() AE,
AE,
∵S△AMN=![]() AMANsin45°,
AMANsin45°,
S△AEF=![]() AEAFsin45°,
AEAFsin45°,
∴![]() =
=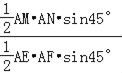 =2,
=2,
∴S△AMN=2S△AEF.


科目:初中数学 来源: 题型:
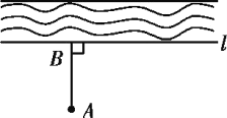
【题目】(1)如图,要把小河里的水引到田地A处,就作AB⊥l(垂足为B),沿AB挖水沟,水沟最短.理由是___________.
(2)把命题“平行于同一直线的两直线平行”写成“如果……,那么……”的形式._____________________________ .
(3)比较大小:![]() ______
______ ![]() .
.
(4)已知![]() 与
与![]() 是同类项,则m-3n的平方根是___.
是同类项,则m-3n的平方根是___.
(5)已知点P的坐标为(3a+6,2﹣a),且点P到两坐标轴的距离相等,则点P的坐标是______.
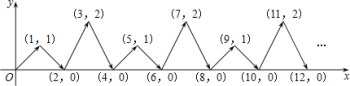
(6) 如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),…,按这样的运动规律,经过第2018次运动后,动点P的坐标是______________
查看答案和解析>>
科目:初中数学 来源: 题型:
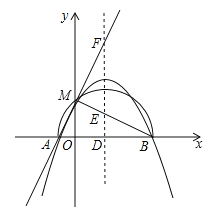
【题目】已知二次函数y=﹣x2+bx+c+1。
(1)当b=1时,求这个二次函数的对称轴的方程;
(2)若c=﹣![]() b2﹣2b,问:b为何值时,二次函数的图象与x轴相切?
b2﹣2b,问:b为何值时,二次函数的图象与x轴相切?
(3)若二次函数的图象与x轴交于点A(x1,0),B(x2,0),且x1<x2,b>0,与y轴的正半轴交于点M,以AB为直径的半圆恰好过点M,二次函数的对称轴l与x轴、直线BM、直线AM分别交于点D、E、F,且满足![]() =
=![]() ,求二次函数的表达式.
,求二次函数的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上三点A,O,B表示的数分别为6,0,-4,动点P从A出发,以每秒6个单位的速度沿数轴向左匀速运动.
(1)当点P到点A的距离与点P到点B的距离相等时,点P在数轴上表示的数是 ;
(2)另一动点R从B出发,以每秒4个单位的速度沿数轴向左匀速运动,若点P、R同时出发,问点P运动多少时间追上点R?
(3)若M为AP的中点,N为PB的中点,点P在运动过程中,线段MN的长度是否发生变化?若发生变化,请你说明理由;若不变,请你画出图形,并求出线段MN的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知 AD 为△ABC 的高线,AD=BC,以 AB 为底边作等腰 Rt△ABE,连接 ED, EC,延长CE 交AD 于F 点,下列结论:①△ADE≌△BCE;②CE⊥DE;③BD=AF;④S△BDE=S△ACE,其中正确的有( )
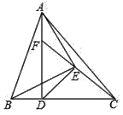
A. ①③B. ①②④C. ①②③④D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
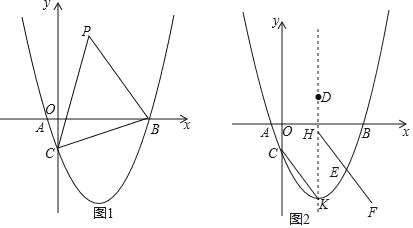
【题目】如图1,在平面直角坐标系中,抛物线 y=![]() x2﹣
x2﹣![]() x﹣
x﹣![]() 与x轴交于A、B、两点(点A在点B的左侧),与y轴交于点C.
与x轴交于A、B、两点(点A在点B的左侧),与y轴交于点C.
(1)判断△ABC形状,并说明理由.
(2)在抛物线第四象限上有一点,它关于x轴的对称点记为点P,点M是直线BC上的一动点,当△PBC的面积最大时,求PM+![]() MC的最小值;
MC的最小值;
(3)如图2,点K为抛物线的顶点,点D在抛物线对称轴上且纵坐标为![]() ,对称轴右侧的抛物线上有一动点E,过点E作EH∥CK,交对称轴于点H,延长HE至点F,使得EF=
,对称轴右侧的抛物线上有一动点E,过点E作EH∥CK,交对称轴于点H,延长HE至点F,使得EF=![]() ,在平面内找一点Q,使得以点F、H、D、Q为顶点的四边形是轴对称图形,且过点Q的对角线所在的直线 是对称轴,请问是否存在这样的点Q,若存在请直接写出点E的横坐标,若不存在,请说明理由.
,在平面内找一点Q,使得以点F、H、D、Q为顶点的四边形是轴对称图形,且过点Q的对角线所在的直线 是对称轴,请问是否存在这样的点Q,若存在请直接写出点E的横坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分8分)某厂制作甲、乙两种环保包装盒。已知同样用6m的材料制成甲盒的个数比制成乙盒的个数少2个,且制成一个甲盒比制作一个乙盒需要多用20%的材料。
(1)求制作每个甲盒、乙盒各用多少材料?
(2)如果制作甲、乙两种包装盒3000个,且甲盒的数量不少于乙盒数量的2倍,那么请写出所需材料总长度![]() 与甲盒数量
与甲盒数量![]() 之间的函数关系式,并求出最少需要多少米材料。
之间的函数关系式,并求出最少需要多少米材料。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是边长为1的正方形,E,F为BD所在直线上的两点.若AE= ![]() ,∠EAF=135°,则以下结论正确的是( )
,∠EAF=135°,则以下结论正确的是( )
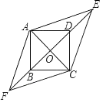
A. DE=1 B. tan∠AFO= ![]() C. AF=
C. AF= ![]() D. 四边形AFCE的面积为
D. 四边形AFCE的面积为 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,表中给出的是某月的月历,任意选取“![]() ”型框中的
”型框中的![]() 个数(如阴影部分所示).请你运用所学的数学知识来研究,则这
个数(如阴影部分所示).请你运用所学的数学知识来研究,则这![]() 个数的和不可能是( )
个数的和不可能是( )
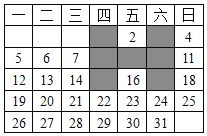
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com