
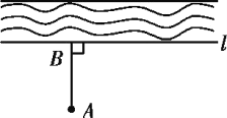
【题目】(1)如图,要把小河里的水引到田地A处,就作AB⊥l(垂足为B),沿AB挖水沟,水沟最短.理由是___________.
(2)把命题“平行于同一直线的两直线平行”写成“如果……,那么……”的形式._____________________________ .
(3)比较大小:![]() ______
______ ![]() .
.
(4)已知![]() 与
与![]() 是同类项,则m-3n的平方根是___.
是同类项,则m-3n的平方根是___.
(5)已知点P的坐标为(3a+6,2﹣a),且点P到两坐标轴的距离相等,则点P的坐标是______.
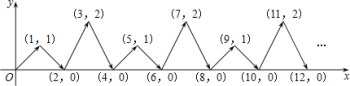
(6) 如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),…,按这样的运动规律,经过第2018次运动后,动点P的坐标是______________
【答案】垂线段最短 如果两条直线都和同一条直线平行,那么这两条直线也互相平行 < ±6 (3,3)或(-6,6) (2018,0)
【解析】
(1)根据垂线段最短解答;
(2)根据命题的形式解答即可;
(3)先化简![]() 即可相比较得到答案;
即可相比较得到答案;
(4)根据同类项的定义得到m、n,即可得到答案;
(5)根据点到坐标轴的距离列方程解答即可;
(6)根据图形发现点是按照四次一循环的规律变化的,找到点坐标的变化规律即可得到答案.
(1)∵AB⊥直线l,
∴AB最短,
理由是:垂线段最短,
故答案为:垂线段最短;
(2)把命题“平行于同一直线的两直线平行”写成“如果……,那么……”的形式是如果两条直线都和第三条直线平行,那么这两条直线也互相平行,
故答案为:如果两条直线都和第三条直线平行,那么这两条直线也互相平行;
(3)∵![]() =
=![]() ,且
,且![]() <
<![]() ,
,
∴![]() <
<![]() ,
,
故答案为:<;
(4)∵![]() 与
与![]() 是同类项,
是同类项,
∴m-2=4,2m+n=2,
∴m=6,n=-10,
∴m-3n=6+30=36,
∴m-3n的平方根是![]() ,
,
故答案为:![]() ;
;
(5)∵点P的坐标为(3a+6,2﹣a),且点P到两坐标轴的距离相等,
∴![]() ,
,
∴![]() 或
或![]() ,
,
∴a=-1或a=-4;
当a=-1时,点P的坐标是(3,3),
当a=-4时,点P的坐标是(-6,6),
故答案为:(3,3)或(-6,6);
(6)第1次运动到点(1,1),
第2次运动到点(2,0),
第3次运动到点(3,2),
第4次运动到点(4,0),
第5次运动到点(5,1),
第6次运动到点(6,0),
第7次运动到点(7,2)
第8次运动到点(8,0),
![]() ,
,
由此得到规律:图形每4次变化一次,且点的横坐标与点运动的次数相同,纵坐标依次是1、0、2、0循环变化,
∵![]() ,
,
∴经过第2018次运动后,动点P的坐标是(2018,0),
故答案为:(2018,0).


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案科目:初中数学 来源: 题型:
【题目】 某新建成学校举行“美化绿化校园”活动,计划购买A、B两种花木共300棵,其中A花木每棵20元,B花木每棵30元.
(1)若购进A,B两种花木刚好用去7300元,则购买了A,B两种花木各多少棵?
(2)如果购买B花木的数量不少于A花木的数量的1.5倍,且购买A、B两种花木的总费用不超过7820元,请问学校有哪几种购买方案?哪种方案最省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在数轴上,一动点![]() 从原点
从原点![]() 出发,沿直线以每秒钟
出发,沿直线以每秒钟![]() 个单位长度的速度来回移动,其移动方式是先向右移动
个单位长度的速度来回移动,其移动方式是先向右移动![]() 个单位长度,再向左移动
个单位长度,再向左移动![]() 个单位长度,又向右移动
个单位长度,又向右移动![]() 个单位长度,再向左移动
个单位长度,再向左移动![]() 个单位长度,又向右移动
个单位长度,又向右移动![]() 个单位长度…
个单位长度…
![]()
(1)求出![]() 秒钟后动点
秒钟后动点![]() 所处的位置;
所处的位置;
(2)如果在数轴上还有一个定点![]() ,且
,且![]() 与原点
与原点![]() 相距20个单位长度,问:动点
相距20个单位长度,问:动点![]() 从原点出发,可能与点
从原点出发,可能与点![]() 重合吗?若能,则第一次与点
重合吗?若能,则第一次与点![]() 重合需多长时间?若不能,请说明理由.
重合需多长时间?若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
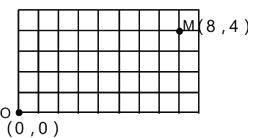
【题目】四个点的坐标分别是: A(0, 3) 、 B(2, 4) 、 C(6, 2) 、 D(5, 0) .
(1)在下面的方格中分别作出 A 、 B 、 C 、 D 四个点的位置;
(2)顺次连结 A 、 B 、 C 、 D 四个点,得到四边形 ABCD ,求四边形 ABCD 的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:如果一个数的平方等于![]() ,记为记
,记为记![]() ,这个数
,这个数![]() 叫做虚数单位,那么形如
叫做虚数单位,那么形如![]() (
(![]() 为实数)的数就叫做复数,
为实数)的数就叫做复数,![]() 叫这个复数的实部,
叫这个复数的实部,![]() 叫做这个复数的虚部。它有如下特点:①它的加,减,乘法运算与整式的加,减,乘法运算类似。例如计算:
叫做这个复数的虚部。它有如下特点:①它的加,减,乘法运算与整式的加,减,乘法运算类似。例如计算:![]() ;
;![]() ②若他们的实部和虚部分别相等,则称这两个复数相等;若它们的实部相等,虚部互为相反数,则称这两个复数共轭,如
②若他们的实部和虚部分别相等,则称这两个复数相等;若它们的实部相等,虚部互为相反数,则称这两个复数共轭,如![]() 的共轭复数为
的共轭复数为![]() 。
。
(1)填空:![]() ;
;![]() 。
。
(2)求![]() 的共轭复数:
的共轭复数:
(3)已知![]() ,其中
,其中![]() 为正整数,求
为正整数,求![]() 的值;
的值;
查看答案和解析>>
科目:初中数学 来源: 题型:
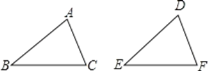
【题目】如图,给出下列四组条件:①AB=DE,BC=EF,AC=DF; ②AB=DE,∠B=∠E,BC=EF;③∠B=∠E,BC=EF,∠C=∠F; ④AB=DE,AC=DF,∠B=∠E.能使△ABC≌△DEF有_____组.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,A、B为x轴上两点,C、D为y轴上的两点,经
中,A、B为x轴上两点,C、D为y轴上的两点,经
过点A、C、B的抛物线的一部分C1与经过点A、D、B的抛物线的一部分C2组合成一条封闭曲线,我们把这条封
闭曲线称为“蛋线”.已知点C的坐标为(0,![]() ),点M是抛物线C2:
),点M是抛物线C2:![]() (
(![]() <0)的顶点.
<0)的顶点.
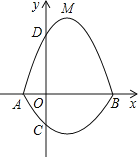
(1)求A、B两点的坐标;
(2)“蛋线”在第四象限上是否存在一点P,使得△PBC的面积最大?若存在,求出△PBC面积的最大值;若不存在,请说明理由;
(3)当△BDM为直角三角形时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知数轴上点A表示的数为﹣1,点B表示的数为3,点P为数轴上一动点.
(1)点A到原点O的距离为 个单位长度;点B到原点O的距离为 个单位长度;线段AB的长度为 个单位长度;
(2)若点P到点A、点B的距离相等,则点P表示的数为 ;
(3)数轴上是否存在点P,使得PA+PB的和为6个单位长度?若存在,请求出PA的长;若不存在,请说明理由?
(4)点P从点A出发,以每分钟1个单位长度的速度向左运动,同时点Q从点B出发,以每分钟2个单位长度的速度向左运动,请直接回答:几分钟后点P与点Q重合?
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如图1,点M,N把线段AB分割成AM,MN和BN,若以AM,MN,BN为边的三角形是一个直角三角形,则称点M,N是线段AB的勾股分割点.
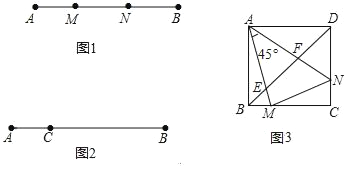
(1)已知点M,N是线段AB的勾股分割点,若AM=3,MN=4求BN的长;
(2)已知点C是线段AB上的一定点,其位置如图2所示,请在BC上画一点D,使C,D是线段AB的勾股分割点(要求尺规作图,保留作图痕迹,画出一种情形即可);
(3)如图3,正方形ABCD中,M,N分别在BC,DC上,且BM≠DN,∠MAN=45°,AM,AN分别交BD于E,F.
求证:①E、F是线段BD的勾股分割点;
②△AMN的面积是△AEF面积的两倍.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com