
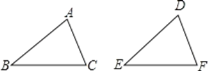
【题目】如图,给出下列四组条件:①AB=DE,BC=EF,AC=DF; ②AB=DE,∠B=∠E,BC=EF;③∠B=∠E,BC=EF,∠C=∠F; ④AB=DE,AC=DF,∠B=∠E.能使△ABC≌△DEF有_____组.
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
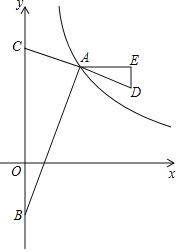
【题目】如图,在平面直角坐标系xOy中,点A是反比例函数y=![]() (x>0,m>1)图象上一点,点A的横坐标为m,点B(0,﹣m)是y轴负半轴上的一点,连接AB,AC⊥AB,交y轴于点C,延长CA到点D,使得AD=AC,过点A作AE平行于x轴,过点D作y轴平行线交AE于点E.
(x>0,m>1)图象上一点,点A的横坐标为m,点B(0,﹣m)是y轴负半轴上的一点,连接AB,AC⊥AB,交y轴于点C,延长CA到点D,使得AD=AC,过点A作AE平行于x轴,过点D作y轴平行线交AE于点E.
(1)当m=3时,求点A的坐标;
(2)DE= ,设点D的坐标为(x,y),求y关于x的函数关系式和自变量的取值范围;
(3)连接BD,过点A作BD的平行线,与(2)中的函数图象交于点F,当m为何值时,以A、B、D、F为顶点的四边形是平行四边形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2017浙江省湖州市)如图,已知∠AOB=30°,在射线OA上取点O1,以O1为圆心的圆与OB相切;在射线O1A上取点O2,以O2为圆心,O2O1为半径的圆与OB相切;在射线O2A上取点O3,以O3为圆心,O3O2为半径的圆与OB相切;…;在射线O9A上取点O10,以O10为圆心,O10O9为半径的圆与OB相切.若⊙O1的半径为1,则⊙O10的半径长是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一个正整数可以表示为两个连续奇数的平方差,那么称该正整数为“和谐数”如(8=32﹣12,16=52﹣32,即8,16均为“和谐数”),在不超过2017的正整数中,所有的“和谐数”之和为( )
A. 255054 B. 255064 C. 250554 D. 255024
查看答案和解析>>
科目:初中数学 来源: 题型:
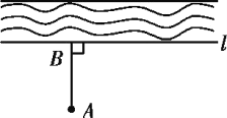
【题目】(1)如图,要把小河里的水引到田地A处,就作AB⊥l(垂足为B),沿AB挖水沟,水沟最短.理由是___________.
(2)把命题“平行于同一直线的两直线平行”写成“如果……,那么……”的形式._____________________________ .
(3)比较大小:![]() ______
______ ![]() .
.
(4)已知![]() 与
与![]() 是同类项,则m-3n的平方根是___.
是同类项,则m-3n的平方根是___.
(5)已知点P的坐标为(3a+6,2﹣a),且点P到两坐标轴的距离相等,则点P的坐标是______.
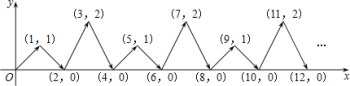
(6) 如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),…,按这样的运动规律,经过第2018次运动后,动点P的坐标是______________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知DE∥BC,BE平分∠ABC,∠C=65°,∠ABC=50°.
(1)求∠BED的度数;
(2)判断BE与AC的位置关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列两段材料,回答下列各题:
材料一:规定:求若干个相同的有理数(均不等于0)的除法运算叫做除方,如:![]() ,
,![]() 等,类比有理数的乘方,我们把
等,类比有理数的乘方,我们把![]() 记作
记作![]() ,读作“2的圈3次方”,
,读作“2的圈3次方”,![]() 记作
记作![]() ,读作“
,读作“![]() 的圈4次方”,一般地,把
的圈4次方”,一般地,把![]() 记作
记作![]() ,读作“
,读作“![]() 的圈
的圈![]() 次方”.
次方”.
材料二:求值:![]() . 解:设
. 解:设![]() ,将等式两边同时乘以2得:
,将等式两边同时乘以2得:![]() 将下式减去上式得
将下式减去上式得![]() 即
即![]()
(1)直接写出计算结果:![]()
(2)我们知道,有理数的减法运算可以转化为加法运算,除法运算可以转化为乘法运算,有理数的除方运算如何转化为乘方运算呢?试一试:将下列运算结果直接写成幂的形式:![]() (
(![]() 且
且![]() 为正整数)
为正整数)
(3)计算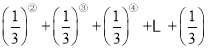
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】教材中的探究:如图1,把两个边长为1的小正方形沿对角线剪开,所得的4个直角三角形拼成一个面积为2的大正方形.由此,得到了一种能在数轴上画出无理数对应点的方法.
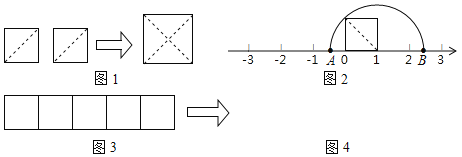
(1)图2中A、B两点表示的数分别为 , ;
(2)请你参照上面的方法,把长为5,宽为1的长方形进行裁剪,拼成一个正方形.
①在图3中画出裁剪线,并在图4位置画出所拼正方形的示意图.
②在数轴上分别标出表示数![]() 以及
以及![]() ﹣3的点,(图中标出必要线段长)
﹣3的点,(图中标出必要线段长)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,抛物线 y=![]() x2﹣
x2﹣![]() x﹣
x﹣![]() 与x轴交于A、B、两点(点A在点B的左侧),与y轴交于点C.
与x轴交于A、B、两点(点A在点B的左侧),与y轴交于点C.
(1)判断△ABC形状,并说明理由.
(2)在抛物线第四象限上有一点,它关于x轴的对称点记为点P,点M是直线BC上的一动点,当△PBC的面积最大时,求PM+![]() MC的最小值;
MC的最小值;
(3)如图2,点K为抛物线的顶点,点D在抛物线对称轴上且纵坐标为![]() ,对称轴右侧的抛物线上有一动点E,过点E作EH∥CK,交对称轴于点H,延长HE至点F,使得EF=
,对称轴右侧的抛物线上有一动点E,过点E作EH∥CK,交对称轴于点H,延长HE至点F,使得EF=![]() ,在平面内找一点Q,使得以点F、H、D、Q为顶点的四边形是轴对称图形,且过点Q的对角线所在的直线 是对称轴,请问是否存在这样的点Q,若存在请直接写出点E的横坐标,若不存在,请说明理由.
,在平面内找一点Q,使得以点F、H、D、Q为顶点的四边形是轴对称图形,且过点Q的对角线所在的直线 是对称轴,请问是否存在这样的点Q,若存在请直接写出点E的横坐标,若不存在,请说明理由.
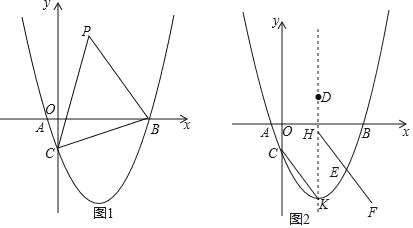
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com