
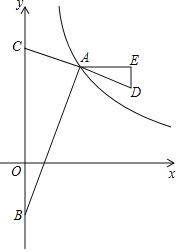
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕxOyжаЃЌЕуAЪЧЗДБШР§КЏЪ§y=![]() ЃЈxЃО0ЃЌmЃО1ЃЉЭМЯѓЩЯвЛЕуЃЌЕуAЕФКсзјБъЮЊmЃЌЕуBЃЈ0ЃЌЉmЃЉЪЧyжсИКАыжсЩЯЕФвЛЕуЃЌСЌНгABЃЌACЁЭABЃЌНЛyжсгкЕуCЃЌбгГЄCAЕНЕуDЃЌЪЙЕУAD=ACЃЌЙ§ЕуAзїAEЦНаагкxжсЃЌЙ§ЕуDзїyжсЦНааЯпНЛAEгкЕуEЃЎ
ЃЈxЃО0ЃЌmЃО1ЃЉЭМЯѓЩЯвЛЕуЃЌЕуAЕФКсзјБъЮЊmЃЌЕуBЃЈ0ЃЌЉmЃЉЪЧyжсИКАыжсЩЯЕФвЛЕуЃЌСЌНгABЃЌACЁЭABЃЌНЛyжсгкЕуCЃЌбгГЄCAЕНЕуDЃЌЪЙЕУAD=ACЃЌЙ§ЕуAзїAEЦНаагкxжсЃЌЙ§ЕуDзїyжсЦНааЯпНЛAEгкЕуEЃЎ
ЃЈ1ЃЉЕБm=3ЪБЃЌЧѓЕуAЕФзјБъЃЛ
ЃЈ2ЃЉDE=ЁЁ ЁЁЃЌЩшЕуDЕФзјБъЮЊЃЈxЃЌyЃЉЃЌЧѓyЙигкxЕФКЏЪ§ЙиЯЕЪНКЭздБфСПЕФШЁжЕЗЖЮЇЃЛ
ЃЈ3ЃЉСЌНгBDЃЌЙ§ЕуAзїBDЕФЦНааЯпЃЌгыЃЈ2ЃЉжаЕФКЏЪ§ЭМЯѓНЛгкЕуFЃЌЕБmЮЊКЮжЕЪБЃЌвдAЁЂBЁЂDЁЂFЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЃП
ЁОД№АИЁПЃЈ1ЃЉЕуAзјБъЮЊЃЈ3ЃЌ6ЃЉЃЛЃЈ2ЃЉ1ЃЌy=![]() ЃЈxЃО2ЃЉЃЛЃЈ3ЃЉm=2ЪБЃЌвдAЁЂBЁЂDЁЂFЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЃЎ
ЃЈxЃО2ЃЉЃЛЃЈ3ЃЉm=2ЪБЃЌвдAЁЂBЁЂDЁЂFЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЃЎ
ЁОНтЮіЁПЃЈ1ЃЉИљОнЬтвтДњШыmжЕМДПЩЧѓЕУЃЛ
ЃЈ2ЃЉРћгУEDЁЮyжсЃЌAD=ACЙЙдьШЋЕШШ§НЧаЮНЋЧѓDEзЊЛЏЮЊЧѓFCЃЌдйРћгУШ§НЧаЮЯрЫЦЧѓГіFCЃЛгУmБэЪОDЕузјБъЃЌРћгУДњШыЯћдЊЗЈЕУЕНyгыxКЏЪ§ЙиЯЕЃЎ
ЃЈ3ЃЉЪ§жЕЩЯЯпЖЮжаЕузјБъЕШгкЖЫЕузјБъЕФЦНОљЪ§ЃЌзјБъЯЕжаЭЌбљПЩЕУЯпЖЮжаЕуКсзнзјБъЗжБ№ЪЧЖЫЕуКсзнзјБъЕФЦНОљЪ§ЃЌРћгУДЫЗНЗЈБэЪОГіFЕузјБъДњШыЃЈ2ЃЉжаКЏЪ§ЙиЯЕЪНМДПЩЃЎ
ЃЈ1ЃЉЕБm=3ЪБЃЌy=![]() ЃЌ
ЃЌ
ЁрЕБx=3ЪБЃЌy=6ЃЌ
ЁрЕуAзјБъЮЊЃЈ3ЃЌ6ЃЉЃЛ
ЃЈ2ЃЉШчЭМЃЌбгГЄEAНЛyжсгкЕуFЃЌ
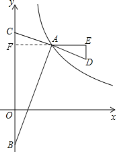
ЁпDEЁЮxжс
ЁрЁЯFCA=ЁЯEDAЃЌЁЯCFA=ЁЯDEAЃЌ
ЁпAD=ACЃЌ
ЁрЁїFCAЁеЁїEDAЃЌ
ЁрDE=CFЃЌ
ЁпAЃЈmЃЌm2ЉmЃЉЃЌBЃЈ0ЃЌЉmЃЉЃЌ
ЁрBF=m2ЉmЉЃЈЉmЃЉ=m2ЃЌAF=mЃЌ
ЁпRtЁїCABжаЃЌAFЁЭxжсЃЌ
ЁрЁїAFCЁзЁїBFAЃЌ
ЁрAF2=CFBFЃЌ
Ёрm2=CFm2ЃЌ
ЁрCF=1ЃЌ
ЁрDE=1ЃЌ
ЙЪД№АИЮЊЃК1ЃЛ
гЩЩЯУцВНжшПЩжЊЃЌЕуEзјБъЮЊЃЈ2mЃЌm2ЉmЃЉЃЌ
ЁрЕуDзјБъЮЊЃЈ2mЃЌm2ЉmЉ1ЃЉЃЌ
Ёрx=2mЃЌ
y=m2ЉmЉ1ЃЌ
ЁрАбm=![]() ДњШыy=m2ЉmЉ1ЃЌ
ДњШыy=m2ЉmЉ1ЃЌ
Ёрy=![]() ЃЈxЃО2ЃЉЃЛ
ЃЈxЃО2ЃЉЃЛ
ЃЈ3ЃЉгЩЬтвтПЩжЊЃЌAFЁЮBD
ЕБADЁЂBFЮЊЦНааЫФБпаЮЖдНЧЯпЪБЃЌ
гЩЦНааЫФБпаЮЖдНЧЯпЛЅЯрЦНЗжПЩЕУAЁЂDКЭBЁЂFЕФКсзјБъЁЂзнзјБъжЎКЭЗжБ№ЯрЕШ
ЩшЕуFзјБъЮЊЃЈaЃЌbЃЉ
Ёрa+0=m+2m
b+ЃЈЉmЃЉ=m2Љm+m2ЉmЉ1
Ёрa=3mЃЌb=2m2ЉmЉ1
ДњШыy=![]() ЃЌЕУ
ЃЌЕУ
2m2ЉmЉ1=![]() ЃЌ
ЃЌ
НтЕУm1=2ЃЌm2=0ЃЈЩсШЅЃЉ
ЕБFDЁЂABЮЊЦНааЫФБпаЮЖдНЧЯпЪБЃЌ
ЭЌРэЩшЕуFзјБъЮЊЃЈaЃЌbЃЉЃЌ
дђa=ЉmЃЌb=1ЉmЃЌдђFЕудкyжсзѓВрЃЌгЩЃЈ2ЃЉПЩжЊЃЌЕуDЫљдкЭМЯѓВЛФмдкyжсзѓВр
ЁрДЫЧщПіВЛДцдкЃЌ
злЩЯЕБm=2ЪБЃЌвдAЁЂBЁЂDЁЂFЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГжабЇЮЊЗсИЛбЇЩњЕФаЃдАЩњЛюЃЌзМБИвЛДЮадЙКТђШєИЩИізуЧђКЭРКЧђЃЈУПИізуЧђЕФМлИёЯрЭЌЃЌУПИіРКЧђЕФМлИёЯрЭЌЃЉЃЌШєЙКТђ3ИізуЧђКЭ2ИіРКЧђЙВаш170дЊЃЌЙКТђ2ИізуЧђКЭ5ИіРКЧђЙВаш260дЊЃЎ
ЃЈ1ЃЉЙКТђвЛИізуЧђЁЂвЛИіРКЧђИїашЖрЩйдЊЃПЃЈЬсЪОЃКСаЗНГЬзщНтД№ЃЉ
ЃЈ2ЃЉИљОнИУжабЇЕФЪЕМЪЧщПіЃЌашвЛДЮадЙКТђзуЧђКЭРКЧђЙВ46ИіЃЌвЊЧѓЙКТђзуЧђКЭРКЧђЕФзмЗбгУВЛГЌЙ§1480дЊЃЌетЫљжабЇзюЖрПЩвдЙКТђЖрЩйИіРКЧђЃПЃЈЬсЪОЃКСаВЛЕШЪННтД№ЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
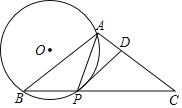
ЁОЬтФПЁПвбжЊЃКШчЭМЃЌдкЁїABCжаЃЌAB=ACЃЌЕуPЪЧЕзБпBCЩЯвЛЕуЧвТњзуPA=PBЃЌЁбOЪЧЁїPABЕФЭтНгдВЃЌЙ§ЕуPзїPDЁЮABНЛACгкЕуDЃЎ
ЃЈ1ЃЉЧѓжЄЃКPDЪЧЁбOЕФЧаЯпЃЛ
ЃЈ2ЃЉШєBC=8ЃЌtanЁЯABC=![]() ЃЌЧѓЁбOЕФАыОЖЃЎ
ЃЌЧѓЁбOЕФАыОЖЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
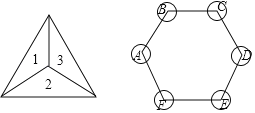
ЁОЬтФПЁПЭМЂйЪЧвЛУЖжЪЕиОљдШЕФе§ЫФУцЬхаЮзДЕФїЛзгЃЌУПИіУцЩЯЗжБ№БъгаЪ§зж1ЃЌ2ЃЌ3ЃЌ4ЃЌЭМЂкЪЧвЛИіе§СљБпаЮЦхХЬЃЌЯжЭЈЙ§жРїЛзгЕФЗНЪНЭцЬјЦхгЮЯЗЃЌЙцдђЪЧЃКНЋетУЖїЛзгжРГіКѓЃЌПДїЛзгЯђЩЯШ§ИіУцЃЈГ§ЕзУцЭтЃЉЕФЪ§зжжЎКЭЪЧМИЃЌОЭДгЭМЂкжаЕФAЕуПЊЪМбизХЫГЪБеыЗНЯђСЌајЬјЖЏМИИіЖЅЕуЃЌЕкЖўДЮДгЕквЛДЮЕФжеЕуДІПЊЪМЃЌАДЕквЛДЮЕФЗНЗЈЬјЖЏЃЎ
ЃЈ1ЃЉЫцЛњжРвЛДЮїЛзгЃЌдђЦхзгЬјЖЏЕНЕуCДІЕФИХТЪЪЧЁЁ ЁЁ
ЃЈ2ЃЉЫцЛњжРСНДЮїЛзгЃЌгУЛЪїзДЭМЛђСаБэЕФЗНЗЈЃЌЧѓЦхзгзюжеЬјЖЏЕНЕуCДІЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁП ФГаТНЈГЩбЇаЃОйааЁАУРЛЏТЬЛЏаЃдАЁБЛюЖЏЃЌМЦЛЎЙКТђAЁЂBСНжжЛЈФОЙВ300ПУЃЌЦфжаAЛЈФОУППУ20дЊЃЌBЛЈФОУППУ30дЊЃЎ
ЃЈ1ЃЉШєЙКНјAЃЌBСНжжЛЈФОИеКУгУШЅ7300дЊЃЌдђЙКТђСЫAЃЌBСНжжЛЈФОИїЖрЩйПУЃП
ЃЈ2ЃЉШчЙћЙКТђBЛЈФОЕФЪ§СПВЛЩйгкAЛЈФОЕФЪ§СПЕФ1.5БЖЃЌЧвЙКТђAЁЂBСНжжЛЈФОЕФзмЗбгУВЛГЌЙ§7820дЊЃЌЧыЮЪбЇаЃгаФФМИжжЙКТђЗНАИЃПФФжжЗНАИзюЪЁЧЎЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
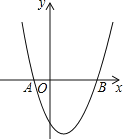
ЁОЬтФПЁПШчЭМЃЌвбжЊХзЮяЯпy=x2-2x-3гыxжсНЛгкAЁЂBСНЕуЃЎ
ЃЈ1ЃЉЕБ0ЃМxЃМ3ЪБЃЌЧѓyЕФШЁжЕЗЖЮЇЃЛ
ЃЈ2ЃЉЕуPЮЊХзЮяЯпЩЯвЛЕуЃЌШєSЁїPAB=10ЃЌЧѓГіДЫЪБЕуPЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
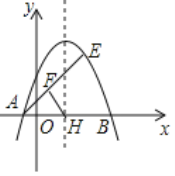
ЁОЬтФПЁПШчЭМЃЌХзЮяЯпy=ЉЃЈxЉ1ЃЉ2+mОЙ§EЃЈ2ЃЌ3ЃЉЃЌгыxжсНЛгкAЁЂBСНЕуЃЈAдкBЕФзѓВрЃЉЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉХзЮяЯпЕФЖдГЦжсгыxжсЕФНЛгкЕуЪЧHЃЌЕуFЪЧAEжаЕуЃЌСЌНгFHЃЎЧѓЯпЖЮFHЕФГЄЃЛ
ЃЈ3ЃЉPЮЊжБЯпAEЩЯЗНХзЮяЯпЩЯЕФЕуЃЎЕБЁїAEPЕФУцЛ§зюДѓЪБЃЎЧѓPЕуЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЁїABCжаЃЌЁЯAЃЌЁЯBЃЌЁЯCЕФЖдБпЗжБ№МЧЮЊ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌгЩЯТСаЬѕМўВЛФмХаЖЈЁїABCЮЊжБНЧШ§НЧаЮЕФЪЧЃЈ ЃЉЃЎ
ЃЌгЩЯТСаЬѕМўВЛФмХаЖЈЁїABCЮЊжБНЧШ§НЧаЮЕФЪЧЃЈ ЃЉЃЎ
AЃЎЁЯA+ЁЯB=ЁЯC
BЃЎЁЯAЁУЁЯBЁУЁЯC =1ЁУ2ЁУ3
CЃЎ![]()
DЃЎ![]() ЁУ
ЁУ![]() ЁУ
ЁУ![]() =3ЁУ4ЁУ6
=3ЁУ4ЁУ6
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
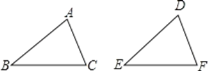
ЁОЬтФПЁПШчЭМЃЌИјГіЯТСаЫФзщЬѕМўЃКЂйAB=DEЃЌBC=EFЃЌAC=DFЃЛ ЂкAB=DEЃЌЁЯB=ЁЯEЃЌBC=EFЃЛЂлЁЯB=ЁЯEЃЌBC=EFЃЌЁЯC=ЁЯFЃЛ ЂмAB=DEЃЌAC=DFЃЌЁЯB=ЁЯEЃЎФмЪЙЁїABCЁеЁїDEFга_____зщЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com