
����Ŀ����֪�������ϣ�һ����![]() ��ԭ��
��ԭ��![]() ��������ֱ����ÿ����
��������ֱ����ÿ����![]() ����λ���ȵ��ٶ������ƶ������ƶ���ʽ���������ƶ�
����λ���ȵ��ٶ������ƶ������ƶ���ʽ���������ƶ�![]() ����λ���ȣ��������ƶ�
����λ���ȣ��������ƶ�![]() ����λ���ȣ��������ƶ�
����λ���ȣ��������ƶ�![]() ����λ���ȣ��������ƶ�
����λ���ȣ��������ƶ�![]() ����λ���ȣ��������ƶ�
����λ���ȣ��������ƶ�![]() ����λ������
���������
![]()
��1�����![]() ���Ӻ�
���Ӻ�![]() ������λ�ã�
������λ�ã�
��2������������ϻ���һ������![]() ����
����![]() ��ԭ��
��ԭ��![]() ���20����λ���ȣ��ʣ�����
���20����λ���ȣ��ʣ�����![]() ��ԭ��������������
��ԭ��������������![]() �غ������ܣ����һ�����
�غ������ܣ����һ�����![]() �غ���ʱ�䣿�����ܣ���˵�����ɣ�
�غ���ʱ�䣿�����ܣ���˵�����ɣ�
���𰸡���1��Q���ک�2����2���ٵ���A��ԭ�����ʱ��ʱ��=390�루6.5���ӣ����ڵ���Aԭ�����ʱ��ʱ��=410�� ��6![]() ���ӣ���
���ӣ���
��������
��1���ȸ���·��=�ٶ���ʱ�����5�����߹���·�̣�Ȼ���������Ҽ���ʽ���㼴�ɵý⣻
��2���ֵ�A��ԭ��������ұ���������ֱ���������߹���·�̣�Ȼ�����ʱ��=·�����ٶȼ��㼴�ɵý⣮
�⣺��1����2��5=10��
����Q�߹���·����1+2+3+4=10��Q���ڣ�1��2+3��4=4��6=��2��
��2��������A��ԭ�����ʱ������Ҫ��n�ε����A����![]() =20�����n=39��
=20�����n=39��
������Q�߹���·����
1+|��2|+3+|��4|+5+��+|��38|+39��
=1+2+3+��+39��
=![]() =780��
=780��
��ʱ��=780��2=390�루6.5���ӣ���
������Aԭ�����ʱ������Ҫ��n�ε����A����![]() =20��
=20��
���n=40��
������Q�߹���·����
1+|��2|+3+|��4|+5+��+39+|��40|��
=1+2+3+��+40��
=![]() =820��
=820��
��ʱ��=820��2=410�� ��6![]() ���ӣ���
���ӣ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�����ֱ��������OAA1��ֱ�DZ�OA��x���ϣ���A1�ڵ�һ���ޣ���OA=1���Ե�A1Ϊֱ�Ƕ��㣬OA1Ϊһֱ�DZ�������ֱ��������OA1A2�����Ե�A2Ϊֱ�Ƕ��㣬OA2Ϊֱ�DZ�������ֱ��������OA2A3�����˹��ɣ����A2018��������_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
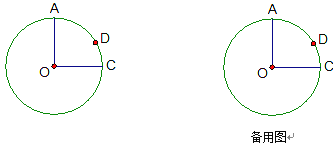
����Ŀ����ͼ����O�İ뾶OA��OC����D��![]() �ϣ���
�ϣ���![]() ��2
��2![]() ��OA��4��
��OA��4��
��1����COD�����������㣻
��2������AD�ij���
��3��P�ǰ뾶OC��һ���㣬����AP��PD�������AP��PD����Сֵ����˵�����ɣ�
������������ʱ���밴���⣬���в���ͼ�Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
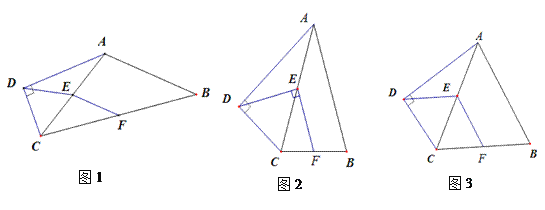
����Ŀ��������ԭ�͡���ͼ1�����ı���ABCD�У���ADC=90����AB=AC.��E��F�ֱ�ΪAC��BC���е㣬����EF��DE����˵����DE=EF��
��̽������ͼ2��������ԭ�͵������£���ACƽ�֡�BAD����DEF=90��ʱ�����BAD�Ĵ�С��
��Ӧ�á���ͼ3��������ԭ�͵������£���AB=2�����ı���CDEF������ʱ��ֱ��д���ı���ABCD�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����Rt��ABC�У���ACB=90�㣬BEƽ����ABC��D�DZ�AB��һ�㣬��BDΪֱ������O������E���ҽ�BC�ڵ�F��
��1����֤��AC����O�����ߣ�
��2����BF=6����O�İ뾶Ϊ5����CE�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����2017�㽭ʡ�����У���ͼ����֪��AOB=30����������OA��ȡ��O1����O1ΪԲ�ĵ�Բ��OB���У�������O1A��ȡ��O2����O2ΪԲ�ģ�O2O1Ϊ�뾶��Բ��OB���У�������O2A��ȡ��O3����O3ΪԲ�ģ�O3O2Ϊ�뾶��Բ��OB���У�����������O9A��ȡ��O10����O10ΪԲ�ģ�O10O9Ϊ�뾶��Բ��OB���У�����O1�İ뾶Ϊ1�����O10�İ뾶����______��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
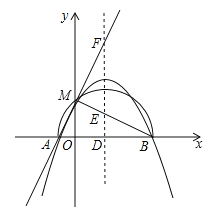
����Ŀ�����壺��ͼ�٣�������y��ax2��bx��c(a��0)��x�ύ��A��B���㣬��P�ڸ���������(P����A��B���㲻�غ�)�������ABP����������AP2��BP2��AB2����Ƶ�PΪ������y��ax2��bx��c(a��0)�Ĺ��ɵ㣮
(1)ֱ��д��������y����x2��1�Ĺ��ɵ�����꣮
(2)��ͼ�ڣ���֪������y��ax2��bx(a��0)��x�ύ��A��B���㣬��P(1�� ![]() )�������ߵĹ��ɵ㣬�������ߵĺ�������ʽ��
)�������ߵĹ��ɵ㣬�������ߵĺ�������ʽ��
(3)��(2)�������£���Q���������ϣ�����������S��ABQ��S��ABP��Q��(���ڵ�P)�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1����ͼ��Ҫ��С�����ˮ�������A��������AB��l(����ΪB)����AB��ˮ����ˮ����̣�������___________��
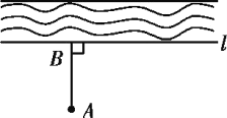
��2�������⡰ƽ����ͬһֱ�ߵ���ֱ��ƽ�С�д�ɡ������������ô����������ʽ��_____________________________ ��
��3���Ƚϴ�С��![]() ______
______ ![]() ��
��
��4����֪![]() ��
��![]() ��ͬ�����m-3n��ƽ������___��
��ͬ�����m-3n��ƽ������___��
��5����֪��P������Ϊ��3a+6��2��a�����ҵ�P����������ľ�����ȣ����P��������______��
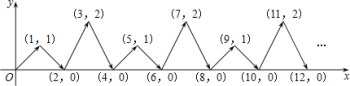
��6�� ��ͼ������P��ƽ��ֱ������ϵ�а�ͼ�м�ͷ��ʾ�����˶�����1�δ�ԭ���˶����㣨1��1������2�ν����˶����㣨2��0������3�ν����˶����㣨3��2�����������������˶����ɣ�������2018���˶�����P��������______________
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y=��x2+bx+c+1��
��1����b=1ʱ����������κ����ĶԳ���ķ��̣�
��2����c=��![]() b2��2b���ʣ�bΪ��ֵʱ�����κ�����ͼ����x�����У�
b2��2b���ʣ�bΪ��ֵʱ�����κ�����ͼ����x�����У�
��3�������κ�����ͼ����x�ύ�ڵ�A��x1��0����B��x2��0������x1��x2��b��0����y��������ύ�ڵ�M����ABΪֱ���İ�Բǡ�ù���M�����κ����ĶԳ���l��x�ᡢֱ��BM��ֱ��AM�ֱ��ڵ�D��E��F��������![]() =
=![]() ������κ����ı���ʽ��
������κ����ı���ʽ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com