
【题目】问题:如何快速计算1+2+3+…+n 的值呢?
(1)探究:令s=1+2+3+…+n①,则s=n+n-1+…+2+1②
①+②得2s=(n+1)(n+1)+…+(n+1)=n![]() (n+1)
(n+1)
因此![]() _________________.
_________________.
(2)应用:
①计算:![]() ________;
________;
②如图1,一串连续的整数1,2,3,4,…,自上往下排列,最上面一行有一个数,以下各行均比上一行多一个数字,若共有15行数字,则最底下一行最左边的数是_______;

③如图2,一串连续的整数-25,-24,-23,…,按图1方式排列,共有14行数字,求图2中所有数字的和.
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:
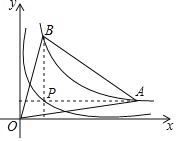
【题目】如图,点P为函数y=![]() (x>0)图象上一点过点P作x轴、y轴的平行线,分别与函数y
(x>0)图象上一点过点P作x轴、y轴的平行线,分别与函数y![]() (x>0)的图象交于点A,B,则△AOB的面积为_____.
(x>0)的图象交于点A,B,则△AOB的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
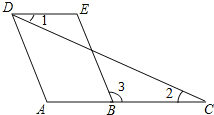
【题目】已知,如图.AD∥BE,∠1=∠2,求证:∠A=∠E.请完成解答过程.
证明:∵AD∥BE(已知)
∴∠A=∠ ( )
又∵∠1=∠2(已知)
∴AC∥ ( )
∴∠3=∠ (两直线平行,内错角相等)
∴∠A=∠E(等量代换)
查看答案和解析>>
科目:初中数学 来源: 题型:
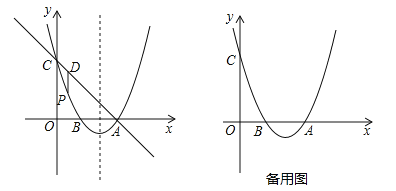
【题目】已知如图,抛物线y=x2+bx+c过点A(3,0),B(1,0),交y轴于点C,点P是该抛物线上一动点,点P从C点沿抛物线向A点运动(点P不与点A重合),过点P作PD∥y轴交直线AC于点D.
(1)求抛物线的解析式;
(2)求点P在运动的过程中线段PD长度的最大值;
(3)△APD能否构成直角三角形?若能请直接写出点P坐标,若不能请说明理由;
(4)在抛物线对称轴上是否存在点M使|MA﹣MC|最大?若存在请求出点M的坐标,若不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为创建足球特色学校,营造足球文化氛围,某学校随机抽取部分八年级学生足球运球的测试成绩作为一个样本,按A,B,C,D四个等级进行统计,制成了如下不完整的统计图.(说明:A级:8分—10分,B级:7分—7.9分,C级:6分—6.9分,D级:1分—5.9分)根据所给信息,解答以下问题:
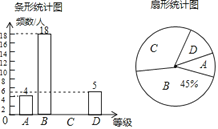
(1)样本容量为 ,C对应的扇形的圆心角是____度,补全条形统计图;
(2)所抽取学生的足球运球测试成绩的中位数会落在____等级;
(3)该校八年级有300名学生,请估计足球运球测试成绩达到![]() 级的学生有多少人?
级的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
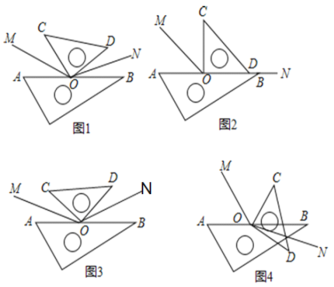
【题目】综合与探究问题背景数学活动课上,老师将一副三角尺按图(1)所示位置摆放,分别作出∠AOC,∠BOD的平分线OM、ON,然后提出如下问题:求出∠MON的度数.
特例探究“兴趣小组”的同学决定从特例入手探究老师提出的问题,他们将三角尺分别按图2、图3所示的方式摆放,OM和ON仍然是∠AOC和∠BOD的角平分线.其中,按图2方式摆放时,可以看成是ON、OD、OB在同一直线上.按图3方式摆放时,∠AOC和∠BOD相等.
(1)请你帮助“兴趣小组”进行计算:图2中∠MON的度数为 °.图3中∠MON的度数为 °.
发现感悟
解决完图2,图3所示问题后,“兴趣小组”又对图1所示问题进行了讨论:
小明:由于图1中∠AOC和∠BOD的和为90°,所以我们容易得到∠MOC和∠NOD的和,这样就能求出∠MON的度数.
小华:设∠BOD为x°,我们就能用含x的式子分别表示出∠NOD和∠MOC度数,这样也能求出∠MON的度数.
(2)请你根据他们的谈话内容,求出图1中∠MON的度数.
类比拓展
受到“兴趣小组”的启发,“智慧小组”将三角尺按图4所示方式摆放,分别作出∠AOC、∠BOD的平分线OM、ON,他们认为也能求出∠MON的度数.
(3)你同意“智慧小组”的看法吗?若同意,求出∠MON的度数;若不同意,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆出租车从![]() 地出发,在一条东西走向的街道上往返,每次行驶的路程(记向东为正)记录如下表所示(
地出发,在一条东西走向的街道上往返,每次行驶的路程(记向东为正)记录如下表所示(![]() ,单位:
,单位:![]() )
)
第一次 | 第二次 | 第三次 | 第四次 |
|
|
|
|
(1)写出这辆出租车每次行驶的方向.
(2)求经过连续4次行驶后,这辆出租车所在的位置.
(3)这辆出租车一共行驶多少路程?
查看答案和解析>>
科目:初中数学 来源: 题型:
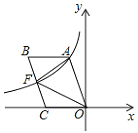
【题目】如图,四边形OABC是平行四边形,边OC在x轴的负半轴上,反比例函数![]() 的图象经过点A与BC的中点F,连接AF,OF,若△AOF的面积为12,则k的值为_______.
的图象经过点A与BC的中点F,连接AF,OF,若△AOF的面积为12,则k的值为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在四边形ABCD中,AD//BC,对角线AC、BD交于点O,且AC=BD,下列四个命题中真命题是( )
A. 若AB=CD,则四边形ABCD一定是等腰梯形;
B. 若∠DBC=∠ACB,则四边形ABCD一定是等腰梯形;
C. 若![]() ,则四边形ABCD一定是矩形;
,则四边形ABCD一定是矩形;
D. 若AC⊥BD且AO=OD,则四边形ABCD一定是正方形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com