
ЁОЬтФПЁПШчЭМЃЌЖўДЮКЏЪ§y=Љx2+bx+cЕФЭМЯѓгыxжсНЛгкЕуA(Љ1ЃЌ0)ЃЌB(2ЃЌ0)ЃЌгыyжсЯрНЛгкЕуCЃЎ
ЃЈ1ЃЉЧѓЖўДЮКЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉШєЕуEЪЧЕквЛЯѓЯоЕФХзЮяЯпЩЯЕФвЛИіЖЏЕуЃЌЕБЫФБпаЮABECЕФУцЛ§зюДѓЪБЃЌЧѓЕуEЕФзјБъЃЌВЂЧѓГіЫФБпаЮABECЕФзюДѓУцЛ§ЃЛ
ЃЈ3ЃЉШєЕуMдкХзЮяЯпЩЯЃЌЧвдкyжсЕФгвВрЃЎЁбMгыyжсЯрЧаЃЌЧаЕуЮЊDЃЎвдCЃЌDЃЌMЮЊЖЅЕуЕФШ§НЧаЮгыЁїAOCЯрЫЦЃЌЧыжБНгаДГіЕуMЕФзјБъЃЎ
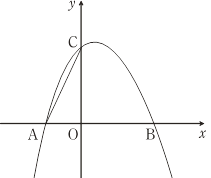
ЁОД№АИЁПЃЈ1ЃЉЖўДЮКЏЪ§ЕФНтЮіЪНЮЊy=Љx2+x+2ЃЛЃЈ2ЃЉЕуEЕФзјБъЮЊ(1ЃЌ2)ЃЌЧвЫФБпаЮABECЕФзюДѓУцЛ§ЮЊ4ЃЛЃЈ3ЃЉЕуMЕФзјБъЮЊ(![]() ЃЌ
ЃЌ ![]() )ЃЌ(
)ЃЌ(![]() ЃЌ
ЃЌ ![]() )ЃЌ(3ЃЌЃ4) .
)ЃЌ(3ЃЌЃ4) .
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉАбAЁЂBЕФзјБъДњШыМДПЩЕУЕНД№АИЃЛ
ЃЈ2ЃЉЩш EЃЈaЃЌbЃЉЃЌЯШБэЪОГіЫФБпаЮABECЕФУцЛ§SЃЌдйХфЗНМДПЩЃЛ
ЃЈ3ЃЉЗжСНжжЧщПіЬжТлЃЌ ![]() ЃЌЛђ
ЃЌЛђ![]() ЃЎ
ЃЎ
ЪдЬтНтЮіЃКЃЈ1ЃЉЁп ЖўДЮКЏЪ§![]() ЕФЭМЯѓгыxжсЯрНЛгкЕуAЃЈЉ1ЃЌ0ЃЉЃЌBЃЈ2ЃЌ0ЃЉЃЌ
ЕФЭМЯѓгыxжсЯрНЛгкЕуAЃЈЉ1ЃЌ0ЃЉЃЌBЃЈ2ЃЌ0ЃЉЃЌ
Ёр![]() ЃЌНтЕУЃК
ЃЌНтЕУЃК ![]() ЃЌЁр ЖўДЮКЏЪ§ЕФНтЮіЪНЮЊ
ЃЌЁр ЖўДЮКЏЪ§ЕФНтЮіЪНЮЊ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉШчЭМ1ЃЎ
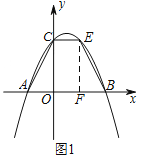
ЁпЖўДЮКЏЪ§ЕФНтЮіЪНЮЊ![]() гыyжсЯрНЛгкЕуCЃЌЁр CЃЈ0ЃЌ2ЃЉЃЌЩш EЃЈaЃЌbЃЉЃЌЧвa >0ЃЌb >0ЃЌЁп AЃЈ-1ЃЌ0ЃЉЃЌBЃЈ2ЃЌ0ЃЉЃЌЁр OA=1ЃЌOB=2ЃЌOC=2ЃЌдђSЫФБпаЮABEC=
гыyжсЯрНЛгкЕуCЃЌЁр CЃЈ0ЃЌ2ЃЉЃЌЩш EЃЈaЃЌbЃЉЃЌЧвa >0ЃЌb >0ЃЌЁп AЃЈ-1ЃЌ0ЃЉЃЌBЃЈ2ЃЌ0ЃЉЃЌЁр OA=1ЃЌOB=2ЃЌOC=2ЃЌдђSЫФБпаЮABEC= ![]() =
= ![]() ЃЌЁп Еу EЃЈaЃЌbЃЉЪЧЕквЛЯѓЯоЕФХзЮяЯпЩЯЕФвЛИіЖЏЕуЃЌЁр
ЃЌЁп Еу EЃЈaЃЌbЃЉЪЧЕквЛЯѓЯоЕФХзЮяЯпЩЯЕФвЛИіЖЏЕуЃЌЁр![]() ЃЌЁр
ЃЌЁр![]() ЃЌЁр ЕБЫФБпаЮABECЕФУцЛ§зюДѓЪБЃЌЕуEЕФзјБъЮЊЃЈ1ЃЌ4ЃЉЃЌЧвЫФБпаЮABECЕФзюДѓУцЛ§ЮЊ4ЃЛ
ЃЌЁр ЕБЫФБпаЮABECЕФУцЛ§зюДѓЪБЃЌЕуEЕФзјБъЮЊЃЈ1ЃЌ4ЃЉЃЌЧвЫФБпаЮABECЕФзюДѓУцЛ§ЮЊ4ЃЛ
ЃЈ3ЃЉШчЭМ2ЃЎ
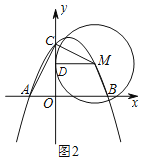
ЩшMЃЈmЃЌnЃЉЃЌЧвm>0ЃЌЁп ЕуMдкЖўДЮКЏЪ§ЕФЭМЯѓЩЯЃЌЁр![]() ЃЌЁп ЁбMгыyжсЯрЧаЃЌЧаЕуЮЊDЃЌЁр ЁЯMDC =90ЁуЃЌЁп вдCЃЌDЃЌMЮЊЖЅЕуЕФШ§НЧаЮгыЁїAOCЯрЫЦЃЌЁр
ЃЌЁп ЁбMгыyжсЯрЧаЃЌЧаЕуЮЊDЃЌЁр ЁЯMDC =90ЁуЃЌЁп вдCЃЌDЃЌMЮЊЖЅЕуЕФШ§НЧаЮгыЁїAOCЯрЫЦЃЌЁр![]() ЃЌЛђ
ЃЌЛђ![]() ЃЌ
ЃЌ
ЂйЕБn >2ЪБЃЌ ![]() ЃЌНтЕУ m1=0ЃЈЩсШЅЃЉЃЌm2=
ЃЌНтЕУ m1=0ЃЈЩсШЅЃЉЃЌm2=![]() ЃЌ Лђm3=0ЃЈЩсШЅЃЉЃЌm4=-1ЃЈЩсШЅЃЉЃЛ
ЃЌ Лђm3=0ЃЈЩсШЅЃЉЃЌm4=-1ЃЈЩсШЅЃЉЃЛ
ЂкЭЌРэПЩЕУЃЌЕБn<2ЪБЃЌm1=0ЃЈЩсШЅЃЉ ЃЌm2=![]() ЃЌЛђm3=0ЃЈЩсШЅЃЉЃЌm4=3ЃЛ
ЃЌЛђm3=0ЃЈЩсШЅЃЉЃЌm4=3ЃЛ
злЩЯЃЌТњзуЬѕМўЕФЕуMЕФзјБъЮЊЃЈ![]() ЃЌ
ЃЌ ![]() ЃЉЃЌЃЈ
ЃЉЃЌЃЈ![]() ЃЌ
ЃЌ ![]() ЃЉЃЌЃЈ3ЃЌ-4ЃЉЃЎ
ЃЉЃЌЃЈ3ЃЌ-4ЃЉЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПНтЗНГЬЃК
(1)x2Ѓ4xЃ1ЃН0; ЁЁЁЁЁЁ
(2)x2ЃЋ3xЃ2ЃН0ЃЛ
(3)2x2ЃЋ3xЃЋ3ЃН0; ЁЁЁЁЁЁ
(4)(2xЃ1)2ЃНx(3xЃЋ2)Ѓ7.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌЁЯAЃН90ЁуЃЌЁЯCЃН30ЁуЃЌADЁЭBCгкDЃЌBEЪЧЁЯABCЕФЦНЗжЯпЃЌЧвНЛADгкPЃЌШчЙћAPЃН2ЃЌдђPЕуЕНABЕФОрРыЮЊ(ЁЁЁЁ)

A.1B.2C.3D.4
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊвЛеХШ§НЧаЮжНЦЌ![]() ШчЭММз
ШчЭММз![]() ЃЌЦфжа
ЃЌЦфжа![]() НЋжНЦЌбиЙ§ЕуBЕФжБЯпелЕўЃЌЪЙЕуCТфЕНABБпЩЯЕФEЕуДІЃЌелКлЮЊ
НЋжНЦЌбиЙ§ЕуBЕФжБЯпелЕўЃЌЪЙЕуCТфЕНABБпЩЯЕФEЕуДІЃЌелКлЮЊ![]() ШчЭМвв
ШчЭМвв![]() дйНЋжНЦЌбиЙ§ЕуEЕФжБЯпелЕўЃЌЕуAЧЁКУгыЕуDжиКЯЃЌелКлЮЊ
дйНЋжНЦЌбиЙ§ЕуEЕФжБЯпелЕўЃЌЕуAЧЁКУгыЕуDжиКЯЃЌелКлЮЊ![]() ШчЭМБћ
ШчЭМБћ![]() дШ§НЧаЮжНЦЌABCжаЃЌ
дШ§НЧаЮжНЦЌABCжаЃЌ![]() ЕФДѓаЁЮЊ______
ЕФДѓаЁЮЊ______![]()

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПНќФъРДЃЌЙВЯэЕЅГЕЗўЮёЕФЭЦГіЃЈШчЭМ1ЃЉЃЌМЋДѓЕФЗНБуСЫГЧЪаЙЋУёТЬЩЋГіааЃЌЭМ2ЪЧФГЦЗХЦФГаЭКХЕЅГЕЕФГЕМмаТЭЖЗХЪБЕФЪОвтЭМЃЈГЕТжАыОЖдМЮЊ30cmЃЉЃЌЦфжаBCЁЮжБЯпlЃЌЁЯBCE=71ЁуЃЌCE=54cmЃЎ
ЃЈ1ЃЉЧѓЕЅГЕГЕзљEЕНЕиУцЕФИпЖШЃЛЃЈНсЙћОЋШЗЕН1cmЃЉ
ЃЈ2ЃЉИљОнОбщЃЌЕБГЕзљEЕНCBЕФОрРыЕїећжСЕШгкШЫЬхПшИпЃЈЭШГЄЃЉЕФ0.85ЪБЃЌзјЦяБШНЯЪцЪЪЃЎаЁУїЕФПшИпЮЊ70cmЃЌЯжНЋГЕзљEЕїећжСзљвЮЪцЪЪИпЖШЮЛжУEЁфЃЌЧѓEEЁфЕФГЄЃЎЃЈНсЙћОЋШЗЕН0.1cmЃЉ
ЃЈВЮПМЪ§ОнЃКsin71ЁуЁж0.95ЃЌcos71ЁуЁж0.33ЃЌtan71ЁуЁж2.90ЃЉ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЙигкxЕФЗНГЬ|x2Љx|Љa=0ЃЌИјГіЯТСаЫФИіНсТлЃКЂйДцдкЪЕЪ§aЃЌЪЙЕУЗНГЬЧЁга2ИіВЛЭЌЕФЪЕИљЃЛ ЂкДцдкЪЕЪ§aЃЌЪЙЕУЗНГЬЧЁга3ИіВЛЭЌЕФЪЕИљЃЛЂлДцдкЪЕЪ§aЃЌЪЙЕУЗНГЬЧЁга4ИіВЛЭЌЕФЪЕИљЃЛЂмДцдкЪЕЪ§aЃЌЪЙЕУЗНГЬЧЁга6ИіВЛЭЌЕФЪЕИљЃЛЦфжае§ШЗЕФНсТлИіЪ§ЪЧЃЈЁЁЁЁЃЉ
A. 1 B. 2 C. 3 D. 4
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвЛДЮКЏЪ§y=Љx+5ЕФЭМЯѓгыЗДБШР§КЏЪ§y=![]() ЃЈkЁй0ЃЉдкЕквЛЯѓЯоЕФЭМЯѓНЛгкAЃЈ1ЃЌnЃЉКЭBСНЕуЃЎЃЈ1ЃЉЧѓЗДБШР§КЏЪ§ЕФНтЮіЪНЃЛ
ЃЈkЁй0ЃЉдкЕквЛЯѓЯоЕФЭМЯѓНЛгкAЃЈ1ЃЌnЃЉКЭBСНЕуЃЎЃЈ1ЃЉЧѓЗДБШР§КЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉдкЕквЛЯѓЯоФкЃЌЕБвЛДЮКЏЪ§y=Љx+5ЕФжЕДѓгкЗДБШР§КЏЪ§y=![]() ЃЈkЁй0ЃЉЕФжЕЪБЃЌаДГіздБфСПxЕФШЁжЕЗЖЮЇЃЎ
ЃЈkЁй0ЃЉЕФжЕЪБЃЌаДГіздБфСПxЕФШЁжЕЗЖЮЇЃЎ
ЃЈ3ЃЉЧѓЁїABOЕФУцЛ§ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌаЁЕКдкИлПкPЕФББЦЋЮї60ЁуЗНЯђЃЌОрИлПк56КЃРяЕФAДІЃЌЛѕДЌДгИлПкPГіЗЂЃЌбиББЦЋЖЋ45ЁуЗНЯђдШЫйЪЛРыИлПкPЃЌ4аЁЪБКѓЛѕДЌдкаЁЕКЕФе§ЖЋЗНЯђЃЌЧѓЛѕДЌЕФКНааЫйЖШЃЎЃЈНсЙћБЃСєИљКХЃЉ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЫФБпаЮABCDжаЃЌЁЯB=ЁЯC=90ЁуЃЌЁЯDABгыЁЯADCЕФЦНЗжЯпЯрНЛгкBCБпЩЯЕФMЕуЃЌдђЯТСаНсТлЃКЂйЁЯAMD=90ЁуЃЛЂкMЮЊBCЕФжаЕуЃЛЂлAB+CD=ADЃЛЂм ![]() ЃЛЂнMЕНADЕФОрРыЕШгкBCЕФвЛАыЃЛЦфжае§ШЗЕФгаЃЈЁЁЁЁЃЉ
ЃЛЂнMЕНADЕФОрРыЕШгкBCЕФвЛАыЃЛЦфжае§ШЗЕФгаЃЈЁЁЁЁЃЉ

A. 2Иі B. 3Иі C. 4Иі D. 5Иі
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com