
【题目】如图,一次函数y=﹣x+5的图象与反比例函数y=![]() (k≠0)在第一象限的图象交于A(1,n)和B两点.(1)求反比例函数的解析式;
(k≠0)在第一象限的图象交于A(1,n)和B两点.(1)求反比例函数的解析式;
(2)在第一象限内,当一次函数y=﹣x+5的值大于反比例函数y=![]() (k≠0)的值时,写出自变量x的取值范围.
(k≠0)的值时,写出自变量x的取值范围.
(3)求△ABO的面积.

【答案】(1)y=![]() ;(2)1<x<4;(3)
;(2)1<x<4;(3)![]() .
.
【解析】
(1)把A点坐标代入一次函数解析式可求得n的值,再代入反比例函数解析式可求得k,即可求得反比例函数解析式;(2)联立两函数解析式,解方程组可求得B点坐标,结合图象可求得满足条件的x的取值范围即可;(3)设一次函数与x轴交于点C,可求得C点坐标,利用S△AOB=S△AOC﹣S△BOC可求得△ABO的面积.
(1)∵点A在一次函数图象上,
∴n=﹣1+5=4,
∴A(1,4),
∵点A在反比例函数图象上,
∴k=4×1=4,
∴反比例函数解析式为y=![]() ;
;
(2)联立两函数解析式可得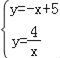 ,解得
,解得![]() 或
或![]() ,
,
∴B点坐标为(4,1),
结合图象可知当一次函数值大于反比例函数值时,x的取值范围为1<x<4;
(3)如图,设一次函数与x轴交于点C,
在y=﹣x+5中,令y=0可求得x=5,
∴C(5,0),即OC=5,
∴S△AOB=S△AOC﹣S△BOC=![]() ×5×4﹣
×5×4﹣![]() ×5×1=
×5×1=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,Rt△AOB中,∠AOB=90°,AO=3BO,OB在x轴上,将Rt△AOB绕点O顺时针旋转至△RtA'OB',其中点B'落在反比例函数y=﹣![]() 的图象上,OA'交反比例函数y=
的图象上,OA'交反比例函数y=![]() 的图象于点C,且OC=2CA',则k的值为( )
的图象于点C,且OC=2CA',则k的值为( )

A. 4 B. ![]() C. 8 D. 7
C. 8 D. 7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一次函数y=mx+4m﹣2.
(1)若这个函数的图象经过原点,求m的值;
(2)若这个函数的图象不过第四象限,求m的取值范围;
(3)不论m取何实数这个函数的图象都过定点,试求这个定点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
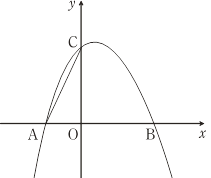
【题目】如图,二次函数y=﹣x2+bx+c的图象与x轴交于点A(﹣1,0),B(2,0),与y轴相交于点C.
(1)求二次函数的解析式;
(2)若点E是第一象限的抛物线上的一个动点,当四边形ABEC的面积最大时,求点E的坐标,并求出四边形ABEC的最大面积;
(3)若点M在抛物线上,且在y轴的右侧.⊙M与y轴相切,切点为D.以C,D,M为顶点的三角形与△AOC相似,请直接写出点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作等边△ABC和等边△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.以下五个结论:

①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP; ⑤∠AOB=60°.
其中正确的结论的个数是( )
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中放置一菱形OABC,已知∠ABC=60°,OA=1.现将菱形OABC沿x轴的正方向无滑动翻转,每次翻转60°,连续翻转2018次,点B的落点依次为B1,B2,B3,B4,…,则B2018的坐标为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E为 BC上的点,F为 CD边上的点,且AE=AF,AB=4,设EC=x,△AEF 的面积为y,则y与x之间的函数关系式是____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)写出阴影部分的面积是_________(写成两数平方差的形式);如图,若将阴影部分裁剪下来,重新拼成一个矩形,它的面积是______(写成多项式乘法的形式);
(2)比较图,图阴影部分的面积,可以得到公式_________;

(3)运用你所得到的公式,计算下列各题:
①![]() ;
;
②(2m+n-p)(2m+n+p)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com