
 已知:如图,DE∥BC,EF∥CD,求证:AD2=AF•AB.
已知:如图,DE∥BC,EF∥CD,求证:AD2=AF•AB. 科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
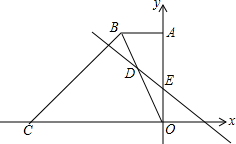 如图,在平面直角坐标系中,直角梯形OABC的边OC,OA分别与x轴,y轴重合,AB∥OC,∠AOC=90°,∠BCO=45°,BC=6$\sqrt{2}$,点C的坐标为(-9,0).
如图,在平面直角坐标系中,直角梯形OABC的边OC,OA分别与x轴,y轴重合,AB∥OC,∠AOC=90°,∠BCO=45°,BC=6$\sqrt{2}$,点C的坐标为(-9,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在长方形ABCD中,边AB、BC的长(AB<BC)是方程x2-7x+12=0的两个根,点P从点A出发,以每秒1个单位的速度沿△ABC边A→B→C→A的方向运动,运动时间为t(秒).
如图,在长方形ABCD中,边AB、BC的长(AB<BC)是方程x2-7x+12=0的两个根,点P从点A出发,以每秒1个单位的速度沿△ABC边A→B→C→A的方向运动,运动时间为t(秒).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
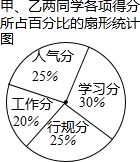 某校八(1)班进行“品学兼优生”的推选工作,经过自荐和第一轮筛选后,甲、乙两名同学进入终选.下表为甲、乙两位同学的得分情况.其中人气分的计算办法是:根据班级同学和部分老师的投票结果,同学一票记3分,老师一票记10分,两个分数相加即为人气分.
某校八(1)班进行“品学兼优生”的推选工作,经过自荐和第一轮筛选后,甲、乙两名同学进入终选.下表为甲、乙两位同学的得分情况.其中人气分的计算办法是:根据班级同学和部分老师的投票结果,同学一票记3分,老师一票记10分,两个分数相加即为人气分. | 候选人 | 人气分 | 学习分 | 行规分 | 工作分 | ||
| 同学投票 | 老师投票 | 分数 | ||||
| 甲 | 25 | 2 | m | 94 | 93 | 95 |
| 乙 | 22 | 3 | 96 | 98 | 90 | 90 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com