
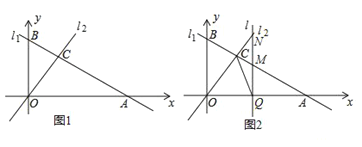
【题目】如图1,直线l1:![]() 与坐标轴分别交于点A,B,与直线l2:
与坐标轴分别交于点A,B,与直线l2:![]() 交于点C.
交于点C.
(1)求A,B两点的坐标;
(2)求△BOC的面积;
(3)如图2,若有一条垂直于x轴的直线l以每秒2个单位的速度从点A出发沿射线AO方向作匀速滑动,分别交直线l1,l2及x轴于点M,N和Q.设运动时间为t(s),连接CQ.
①当OA=2MN时,求t的值;
②试探究是否存在点Q,使得以△OQC为等腰三角形?若存在,请直接写出t的值;若不存在,请说明理由
【答案】A(6,0),B(0,3);(2)△BOC的面积为3;(3)①t=1或t=3,②t=1,2,![]() ,
,![]()
【解析】
(1)令x=0得到y=3,令y=0,得到x=6,从而可得A、B点的坐标;
(2)构建方程组确定点C坐标即可解决问题;
(3)①根据绝对值方程即可解决问题;
②分为三种情况,画出图形,根据等腰三角形的性质求出即可.
(1)对于直线![]() ,令x=0得到y=3,令y=0,得到x=6,
,令x=0得到y=3,令y=0,得到x=6,
∴A(6,0),B(0,3).
(2)由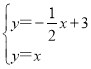 ,解得
,解得![]() ,
,
∴C(2,2),
∴S△OBC=![]() ×3×2=3
×3×2=3
(3)①设M(6-2t,-![]() (6-2t)+3),N(6-2t,6-2t),
(6-2t)+3),N(6-2t,6-2t),
∴MN=|-![]() (6-2t)+3-(6-2t)|=|3t-6|,
(6-2t)+3-(6-2t)|=|3t-6|,
∵OA=2MN,
∴6=2|3t-6|,
解得t=1或3;
②分三种情况:
i)、CO为底时,Q为顶点时,如图①,
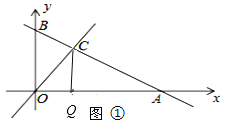
当∠COQ=45°,CQ=OQ,
∵C(2,2),
∴OQ=CQ=2,
∴AQ=OA-OQ=6-2=4,
∴t=4÷2=2(s);
ii)当CO为腰时,C为顶点时,如图②,过C作CM⊥OA于M,
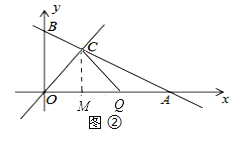
∵C(2,2),
∴CM=OM=2,
∴QM=OM=2,
∴AQ=OA-OQ=2,
∴t=2÷2=1(s);
iii)当CO为腰时,O为顶点时,如图③:
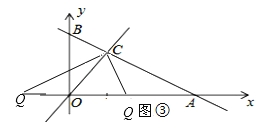
OQ=OC=2![]() ,
,
AQ=AO-OQ=6-2![]() 或AQ=AO+OQ=6+2
或AQ=AO+OQ=6+2![]() .
.
∴t=![]() 或t=
或t=![]() .
.
综上所述:t的值为1或2或![]() 或
或![]() .
.


 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:初中数学 来源: 题型:
【题目】我们知道,假分数可以化为整数与真分数的和的形式.例如:![]() .在分式中,对于只含有一个字母的分式,当分子的次数大于或等于分母的次数时,我们称之为“假分式”;当分子的次数小于分母的次数时,我们称之为“真分式”.例如:像
.在分式中,对于只含有一个字母的分式,当分子的次数大于或等于分母的次数时,我们称之为“假分式”;当分子的次数小于分母的次数时,我们称之为“真分式”.例如:像![]() ,
,![]() ,…这样的分式是假分式;像
,…这样的分式是假分式;像![]() ,
,![]() ,…这样的分式是真分式.类似的,假分式也可以化为整式与真分式的和的形式. 例如:
,…这样的分式是真分式.类似的,假分式也可以化为整式与真分式的和的形式. 例如: ![]() ’
’
![]() .
.
(1)将分式![]() 化为整式与真分式的和的形式;
化为整式与真分式的和的形式;
(2)如果分式![]() 的值为整数,求x的整数值.
的值为整数,求x的整数值.
查看答案和解析>>
科目:初中数学 来源: 题型:
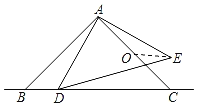
【题目】在平面直角坐标系中,点A(0,6),B(8,0),AB=10,如图作∠DBO=∠ABO,∠CAy=∠BAO,BD交y轴于点E,直线DO交AC于点C.
(1)①求证:△ACO≌△EDO;②求出线段AC、BD的位置关系和数量关系;
(2)动点P从A出发,沿A﹣O﹣B路线运动,速度为1,到B点处停止运动;动点Q从B出发,沿B﹣O﹣A运动,速度为2,到A点处停止运动.二者同时开始运动,都要到达相应的终点才能停止.在某时刻,作PE⊥CD于点E,QF⊥CD于点F.问两动点运动多长时间时△OPE与△OQF全等?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,海中有一小岛P,在距小岛P的![]() 海里范围内有暗礁,一轮船自西向东航行,它在A处时测得小岛P位于北偏东60°,且A、P之间的距离为32海里,若轮船继续向正东方向航行,轮船有无触礁危险?请通过计算加以说明.如果有危险,轮船自A处开始至少沿东偏南多少度方向航行,才能安全通过这一海域?
海里范围内有暗礁,一轮船自西向东航行,它在A处时测得小岛P位于北偏东60°,且A、P之间的距离为32海里,若轮船继续向正东方向航行,轮船有无触礁危险?请通过计算加以说明.如果有危险,轮船自A处开始至少沿东偏南多少度方向航行,才能安全通过这一海域?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数y=kx+4的图象经过点(-3,-2).
(1)求这个函数关系式;
(2)判断点(-5,3)是否在此函数的图象上,说明理由;
(3)求出该函数图像与坐标轴围成的三角形的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,AB=AC=2,O为AC中点,若点D在直线BC上运动,连接OE,则在点D运动过程中,则OE的最小值是为( )
A.![]() B.0.25C.1D.2
B.0.25C.1D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一块直角三角形的绿地,量得两直角边长分别为5m,12m.现在要将绿地扩充成等腰三角形绿地,且扩允部分是以12m为直角边的直角三角形,求扩充部分三角形绿地的面积.(如图备用)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设a,b,c是△ABC的三条边,关于x的方程![]() x2+
x2+![]() x+c-
x+c-![]() a=0有两个相等的实数根,方程3cx+2b=2a的根为x=0.
a=0有两个相等的实数根,方程3cx+2b=2a的根为x=0.
(1)试判断△ABC的形状;
(2)若a,b为方程x2+mx-3m=0的两个根,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程![]()
(1)若方程有两个相等的实数根,求m的值,并求出此时方程的根;
(2)是否存在正数m,使方程的两个实数根的平方和等于224.若存在,求出满足条件的m的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com