
已知二次函数y=x2-ax-2a2(a为常数,且a≠0).
(1)证明该二次函数的图像与x轴的正半轴、负半轴各有一个交点;
(2)若该二次函数的图像与y轴的交点坐标为(0,-2),试求该函数图像的顶点
坐标.
解:(1)
法一:y=x2-ax-2a2 =(x+a)(x-2a),
令y=0,则x1=-a,x2=2a, …………2分
∵a≠0,x1、x2的值必为一正一负, …………3分
∴该二次函数的图像与x轴的正半轴、负半轴各有一个交点; …………4分
法二:由y=0得:x2-ax-2a2 =0(*),
∵△=(-a)2-4×1×(-2a2)=9a2,a≠0,
∴△>0,∴(*)有二个不相等的值数根.设二实数根为x1,x2,…………2分
∵x1x2=-2a2<0,∴(*)有2个异号的实数根
∴该二次函数的图像与x轴的正半轴、负半轴各有一个交点;…………4分
(2)由题意,得-2a2=-2 ,所以a=1或-1. …………5分
当a=1时,y=x2-x-2=(x-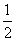 )2-
)2-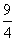 ,顶点坐标为(
,顶点坐标为(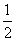 ,-
,-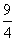 ) …………6分
) …………6分
当a=-1时,y=x2+x-2=(x+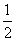 )2-
)2-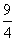 ,顶点坐标为(-
,顶点坐标为(-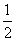 ,-
,-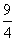 )…………7分
)…………7分
该函数图像的顶点坐标为(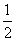 ,-
,-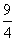 )或(-
)或(-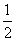 ,-
,-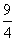 ).…………8分
).…………8分


 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:初中数学 来源: 题型:
小王参加某企业招聘测试,他的笔试,面试、技能操作得分分别为85分,80分,90分,若依次按照2:3:5的比例确定成绩,则小王的成绩是( )
A. 255分 B. 84分 C. 84.5分 D.86分
查看答案和解析>>
科目:初中数学 来源: 题型:
为满足市场需求,某超市在五月初五“端午节”来临前夕,购进一种品牌粽子,每盒进价是40元,超市规定每盒售价不得少于45元. 根据以往销售经验发现:当售价定为每盒45元时,每天可卖出700盒,每盒售价每提高1元,每天要少卖出20盒.
(1)试求出每天的销售量y(盒)与每盒售价x(元)之间的函数关系式;
(2)当每盒售价定为多少元时,每天销售的利润P(元)最大?最大利润是多少?
(3)为稳定物价,有关管理部门限定:这种粽子的每盒售价不得高于58元. 如果超市想要每天获得不低于6000元的利润,那么超市每天至少销售粽子多少盒?
查看答案和解析>>
科目:初中数学 来源: 题型:
一个不透明的袋中,装有编号为①、②、③、④的四个球,他们除了编号外其余
都相同.
(1)从袋中任意摸出一个球,摸到编号为奇数的球的概率为 ;
(2)从袋中任意摸出两个球,求摸到的球编号都为奇数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
南京青奥会期间约有1020000人次参与了青奥文化教育活动.将数据1020000用科学记数法表示为
A.10.2×105 B.1.02×105 C.1.02×106 D.1.02×107
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在△ABC中,∠A=90°,AB=AC=12 cm,半径为4 cm的⊙O与AB、AC两边都相切,与BC交于点D、E.点P从点A出发,沿着边AB向终点B运动,点Q从点B出发,沿着边BC向终点C运动,点R从点C出发,沿着边CA向终点A运动.已知点P、Q、R同时出发,运动速度分别是1 cm/s、x cm/s、1.5 cm/s,运动时间为t s.
(1)求证:BD=CE;
(2)若x=3,当△PBQ∽△QCR时,求t的值;
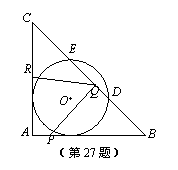 (3)设△PBQ关于直线PQ对称的图形是△PB'Q,求当t和x分别为何值时,点B'与圆心O恰好重合.
(3)设△PBQ关于直线PQ对称的图形是△PB'Q,求当t和x分别为何值时,点B'与圆心O恰好重合.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com