
如图,在△ABC中,∠A=90°,AB=AC=12 cm,半径为4 cm的⊙O与AB、AC两边都相切,与BC交于点D、E.点P从点A出发,沿着边AB向终点B运动,点Q从点B出发,沿着边BC向终点C运动,点R从点C出发,沿着边CA向终点A运动.已知点P、Q、R同时出发,运动速度分别是1 cm/s、x cm/s、1.5 cm/s,运动时间为t s.
(1)求证:BD=CE;
(2)若x=3,当△PBQ∽△QCR时,求t的值;
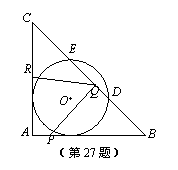 (3)设△PBQ关于直线PQ对称的图形是△PB'Q,求当t和x分别为何值时,点B'与圆心O恰好重合.
(3)设△PBQ关于直线PQ对称的图形是△PB'Q,求当t和x分别为何值时,点B'与圆心O恰好重合.
(1)证明:连接AO并延长交BC于点H.连接OE、OD.
∵⊙O与AB、AC两边都相切,
∴点O到AB、AC两边的距离相等.
∴AH是∠CAB的平分线.
∵AB=AC,
∴AH⊥BC,AH平分BC.
∵OE=OD,OH⊥ED,
∴OH平分ED.
∵CE=CH-EH,BD=BH-DH,
且CH=BH,EH=DH,
∴ BD=CE. 3分


(2)解:在Rt△ABC中,BC=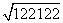 =12
=12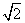 .
.
∵△PBQ∽△QCR,∴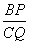 =
=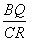 ,即
,即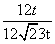 =
=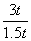 .解得t=
.解得t=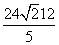 . 6分
. 6分
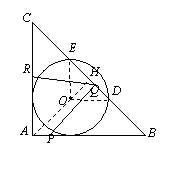
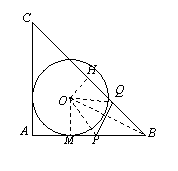
(3)解:设⊙O与AB相切于点M,连接OM、OB、OP、OQ,H参考(1)中作法.
∵点O与点B关于PQ对称,
∴PQ垂直平分BO.
∴OP=BP,OQ=BQ.
∵⊙O与AB相切于点M,∴OM⊥AB.
设BP=a,在Rt△OMP中,(12-4-a)2+42=a2,解得a=5;
设BQ=b,在Rt△OHB中,(6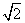 -b)2+(2
-b)2+(2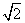 )2=b2,解得b=
)2=b2,解得b=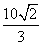 .
.
t=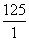 =7 s. x=
=7 s. x=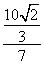 =
=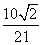 cm.
cm.


 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:初中数学 来源: 题型:
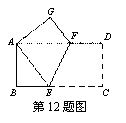
如图,矩形纸片ABCD中,AB=4,BC=8,将纸片沿EF折叠,使点C与点A重合,则下列结论错误的是( ).
A.AF=AE B.△ABE≌△AGF
C.EF=2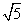 D.AF=EF
D.AF=EF
查看答案和解析>>
科目:初中数学 来源: 题型:
已知二次函数y=x2-ax-2a2(a为常数,且a≠0).
(1)证明该二次函数的图像与x轴的正半轴、负半轴各有一个交点;
(2)若该二次函数的图像与y轴的交点坐标为(0,-2),试求该函数图像的顶点
坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在正方形ABCD中,点E在对角线AC上,点F在边BC上,连接BE、DF,DF交对角线AC于点G,且DE=DG.
(1)求证:AE=CG;
(2)试判断BE和DF的位置关系,并说明理由.
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
下列命题中,假命题的是
A.两组对边分别相等的四边形是平行四边形
B.一组对边平行且相等的四边形是平行四边形
C.一组对边平行,一组对角相等的四边形是平行四边形
D.一组对边相等,一组对角相等的四边形是平行四边形
查看答案和解析>>
科目:初中数学 来源: 题型:
能判断四边形是平行四边形的是( )
A.一组对边平行,另一组对边相等
B.一组对边平行,一组对角相等
C.一组对边平行,一组邻角互补
D.一组对边相等,一组邻角相等
查看答案和解析>>
科目:初中数学 来源: 题型:
在Rt△ABC中,∠C=90°,AB= 8.
(1)当∠B = 60° 时,BC = ;
(2)当其中有一个锐角为30°,动点P在直线BC上(不与点B,C重合),且∠PAC=60°,
则BP的长为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com