练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，四边形ABCD为⊙O的内接四边形，连接AC、BO，已知∠CAB＝36°，∠ABO＝30°，则∠D＝    °．


    96    

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    如图，边长为8的正方形OABC的两边在坐标轴上，以点C为顶点的抛物线经过点A，点P是抛物线上点A、C间的一个动点（含端点），过点P作PF⊥BC于点F. 点D、E的坐标分别为（0，6），（-4，0），连接PD，PE，DE.

       （1）请直接写出抛物线的解析式；

    （2）小明探究点P的位置发现：当点P与点A或点C重合时，PD与PF的差为定值. 进而猜想：对于任意一点P，PD与PF的差为定值. 请你判断该猜想是否正确，并说明理由；

    （3）小明进一步探究得出结论：若将“使△PDE的面积为整数”的点P记作“好点”，则存在多个“好点”，且使△PDE的周长最小的点P也是一个“好点”.

         请直接写出所有“好点”的个数，并求出△PDE的周长最小时“好点”的坐标.

     


     

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    正比例函数y1＝k1x的图像与反比例函数y2＝的图象相交于点A（－1，2）和点B ．

    当y1＜y2时，自变量x的取值范围是       ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    南京青奥会期间约有1020000人次参与了青奥文化教育活动．将数据1020000用科学记数法表示为

     　　　　A．10.2×105　B．1.02×105    C．1.02×106                               D．1.02×107

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    计算：sin45°＋－＝        ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    在一个不透明的口袋里装有四个球，这四个球上分别标记数字－3、－1、0、2，除数字不同外，这四个球没有任何区别．

       （1）从中任取一球，求该球上标记的数字为正数的概率；

       （2）从中任取两球，将两球上标记的数字分别记为x、y，求点（x，y）位于第二象限的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在△ABC中，∠A＝90°，AB＝AC＝12 cm，半径为4 cm的⊙O与AB、AC两边都相切，与BC交于点D、E．点P从点A出发，沿着边AB向终点B运动，点Q从点B出发，沿着边BC向终点C运动，点R从点C出发，沿着边CA向终点A运动．已知点P、Q、R同时出发，运动速度分别是1 cm/s、x cm/s、1.5 cm/s，运动时间为t s.

      （1）求证：BD＝CE；

      （2）若x＝3，当△PBQ∽△QCR时，求t的值；

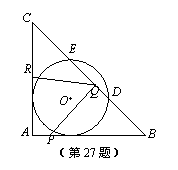      （3）设△PBQ关于直线PQ对称的图形是△PB'Q，求当t和x分别为何值时，点B'与圆心O恰好重合．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    解方程组

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知∠1＝40°，则∠1的余角的度数是（    ）

    A．40°；         B．50°；           C．140°；        D．150°.

    查看答案和解析>>

    同步练习册答案