
如图,在正方形ABCD中,点E在对角线AC上,点F在边BC上,连接BE、DF,DF交对角线AC于点G,且DE=DG.
(1)求证:AE=CG;
(2)试判断BE和DF的位置关系,并说明理由.
 |
解:(1)证明:在正方形ABCD中,
∵AD=CD,
∴∠DAE=∠DCG,
∵DE=DG, ∴∠DEG=∠DGE,
∴∠AED=∠CGD.
在△AED和△CGD中,
∵∠DAE=∠DCG,∠AED=∠CGD,DE=DG,
∴△AED≌△CGD,
∴AE=CG. 4分
(2)解法一:BE∥DF,理由如下:
在正方形ABCD中,AB∥CD,AB=CD,
∴∠BAE=∠DCG.
又∵AE=CG,
∴△AEB≌△CGD,
∴∠AEB=∠CGD.
∵∠CGD=∠EGF,
∴∠AEB=∠EGF,
∴ BE∥DF. 9分
解法二:BE∥DF,理由如下:
在正方形ABCD中,
∵AD∥FC,
∴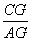 =
=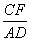 .
.
∵CG=AE,
∴AG=CE.
又∵在正方形ABCD中,AD=CB,
∴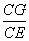 =
=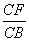 .
.
又∵∠GCF=∠ECB,
∴△CGF∽△CEB,
∴∠CGF=∠CEB,
∴ BE∥DF. 9分


科目:初中数学 来源: 题型:
如图,在△ABC中,∠B=30°,BC的垂直平分线交AB于点E,垂足为D,CE平分∠ACB,若BE=2,则AE的长为(
).
A.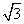 B.1 C.
B.1 C. D.2
D.2
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
一个不透明的袋中,装有编号为①、②、③、④的四个球,他们除了编号外其余
都相同.
(1)从袋中任意摸出一个球,摸到编号为奇数的球的概率为 ;
(2)从袋中任意摸出两个球,求摸到的球编号都为奇数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在△ABC中,∠A=90°,AB=AC=12 cm,半径为4 cm的⊙O与AB、AC两边都相切,与BC交于点D、E.点P从点A出发,沿着边AB向终点B运动,点Q从点B出发,沿着边BC向终点C运动,点R从点C出发,沿着边CA向终点A运动.已知点P、Q、R同时出发,运动速度分别是1 cm/s、x cm/s、1.5 cm/s,运动时间为t s.
(1)求证:BD=CE;
(2)若x=3,当△PBQ∽△QCR时,求t的值;
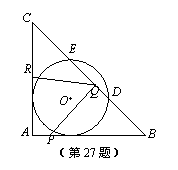 (3)设△PBQ关于直线PQ对称的图形是△PB'Q,求当t和x分别为何值时,点B'与圆心O恰好重合.
(3)设△PBQ关于直线PQ对称的图形是△PB'Q,求当t和x分别为何值时,点B'与圆心O恰好重合.
查看答案和解析>>
科目:初中数学 来源: 题型:
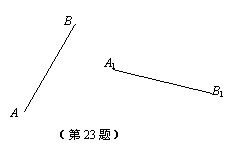
如图,线段AB绕点O顺时针旋转一定的角度得到线段A1B1.
(1)请用直尺和圆规作出旋转中 心O(不写作法,保留作图痕迹);
心O(不写作法,保留作图痕迹);
(2)连接OA、OA1、OB、OB1,根据旋转的性质用符号语言写出2条不同类型的正确结论;
(3)针对第(2)问中的图形,添加一定的条件,可以求出线段AB扫过的面积.(不再添加字母和辅助线,线段的长用a、b、c…表示,角的度数用α、β、γ…表示).
你添加的条件是 ,线段AB扫过的面积是 .
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com