
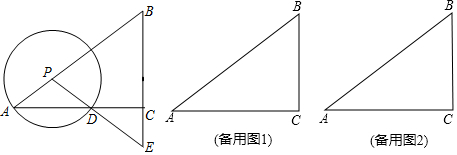
���� ��1����PH��AC������ΪH��������֪�����õ�AB=5��AC=4����ƽ���߷��߶γɱ��������õ�$\frac{PH}{BC}=\frac{PA}{AB}$���õ�PH=$\frac{3}{5}$�����ǵõ����ۣ�
��2������P���C����ʱ����C�ڡ�P�ڣ����ǵõ���D��AC���ӳ����ϵ�P��PG��AC������ΪG����PA=x����PG=$\frac{3}{5}$x��AG=DG=$\frac{4}{5}$x��CD=$\frac{8}{5}$x-4��CG=4-$\frac{4}{5}$x������$\frac{CE}{PG}$=$\frac{DC}{DG}$���õ�CE=$\frac{6}{5}$x-3������PA-CE=PC��
�з��̵õ����ۣ�
��3��������ǵ����ʵõ���ABC=��PEC���������õ���PEC=��EBP�����ݵ��������ε��ж��õ�PB=PE�����������ε���λ�ߵ����ʵõ�PQ��AC���ɵõ����ۣ�
��� �⣺��1����ͼ1����PH��AC������ΪH��
��PH��Բ�ģ�
��AH=DH��
�ߡ�ACB=90�㣬
��PH��BC��
��cosB=$\frac{3}{5}$��BC=3��
��AB=5��AC=4��
��PH��BC��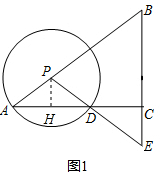
��$\frac{PH}{BC}=\frac{PA}{AB}$��
��$\frac{PH}{3}=\frac{1}{5}$��
��PH=$\frac{3}{5}$��
��AH=DH=$\frac{4}{5}$��
��DC=$\frac{12}{5}$��
�֡�$\frac{PH}{CE}$=$\frac{DH}{DC}$��
��$\frac{\frac{3}{5}}{CE}$=$\frac{\frac{4}{5}}{\frac{12}{5}}$��
��CE=$\frac{9}{5}$��
��2������P���C����ʱ����C�ڡ�P�ڣ�
���D��AC���ӳ�����
��P��PG��AC������ΪG����PA=x����PG=$\frac{3}{5}$x��AG=DG=$\frac{4}{5}$x��CD=$\frac{8}{5}$x-4��CG=4-$\frac{4}{5}$x��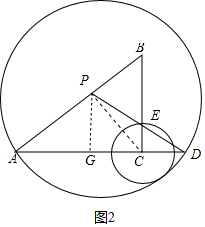
��$\frac{CE}{PG}$=$\frac{DC}{DG}$��
��$\frac{CE}{\frac{3}{5}x}$=$\frac{\frac{8}{5}x-4}{\frac{4}{5}x}$��
��CE=$\frac{6}{5}$x-3��
�ߡ�P���C���У�
��PA-CE=PC��
��x-��$\frac{6}{5}$x-3��=$\sqrt{��\frac{3}{5}x��^{2}+��4-\frac{4}{5}x��^{2}}$��
��24x2-130x+175=0��
��x1=$\frac{35}{12}$��x2=$\frac{5}{2}$��
�൱��P���C����ʱ����P�İ뾶Ϊ$\frac{35}{12}$��
��3���ߡ�ABC+��A=90�b����PEC+��CDE=90�b��
�ߡ�A=��PDA��
���ABC=��PEC
�ߡ�ABC=��EBP��
���PEC=��EBP��
��PB=PE��
�ߵ�QΪ�߶�BE���е㣬
��PQ��BC����PQ��AC
�൱PE��CFʱ���ı���PDCF��ƽ���ı��Σ�
��PF=CD��
����P�ڱ�AB����ʱ��x=4-$\frac{8}{5}$x��x=$\frac{20}{13}$��
����P�ڱ�AB���ӳ�����ʱ��x=$\frac{8}{5}$x-4��x=$\frac{20}{3}$��
������������PE��CFʱ��AP�ij�Ϊ$\frac{20}{13}$��$\frac{20}{3}$��
���� ���⿼����Բ���ۺ��⣺����������Բ���е����ʺ����������Ƶ��ж������ʣ������ù��ɶ��������ƱȽ��м��μ��㣻�����÷������۵�˼������Ǵ���ؼ�����Ŀ���ۺ��Ժ�ǿ��ǣ������֪ʶ��϶࣬��ѧ�����ۺϽ�������Ҫ��ܸߣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��������y=mx2-4mx��ͼ����x�ύ�ڵ�O��A����ֱ֪��l�Ľ���ʽΪy=kx��k��0������A����l�ĶԳƵ�Ϊ��B��
��ͼ��������y=mx2-4mx��ͼ����x�ύ�ڵ�O��A����ֱ֪��l�Ľ���ʽΪy=kx��k��0������A����l�ĶԳƵ�Ϊ��B���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
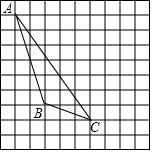 ��ͼ����ABC�ڷ���ֽ��
��ͼ����ABC�ڷ���ֽ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
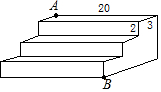 ��ͼ����һ������̨�ף�����ÿһ���ij��������߷ֱ�Ϊ20dm��3dm��2dm��A��B�����̨��������ԵĶ˵㣬A����һֻ���ϣ��뵽B��ȥ�Կɿڵ�ʳ�����������̨��������B������·���ǣ�������
��ͼ����һ������̨�ף�����ÿһ���ij��������߷ֱ�Ϊ20dm��3dm��2dm��A��B�����̨��������ԵĶ˵㣬A����һֻ���ϣ��뵽B��ȥ�Կɿڵ�ʳ�����������̨��������B������·���ǣ�������| A�� | 20$\sqrt{3}$ | B�� | 25$\sqrt{2}$ | C�� | 20 | D�� | 25 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
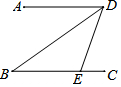 ��ͼ��AD��BC����E��BC�ϣ�DBƽ�֡�ADE������DBE=40�㣬���DEC=��������
��ͼ��AD��BC����E��BC�ϣ�DBƽ�֡�ADE������DBE=40�㣬���DEC=��������| A�� | 20�� | B�� | 40�� | C�� | 60�� | D�� | 80�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
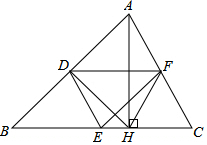 ��֪����ͼ���ڡ�ABC�У�D��E��F�ֱ��Ǹ��ߵ��е㣬AH�Ǹߣ���֤����DEF=��DHF��
��֪����ͼ���ڡ�ABC�У�D��E��F�ֱ��Ǹ��ߵ��е㣬AH�Ǹߣ���֤����DEF=��DHF���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
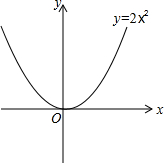 ��ƽ��ֱ������ϵxOy�У����ڵ�P��x��y���������Q��x��y�䣩������������y��=$\left\{\begin{array}{l}{x-y����x��yʱ��}\\{y-x����x��yʱ��}\end{array}\right.$����ô�Ƶ�QΪ��P�ġ������㡱��
��ƽ��ֱ������ϵxOy�У����ڵ�P��x��y���������Q��x��y�䣩������������y��=$\left\{\begin{array}{l}{x-y����x��yʱ��}\\{y-x����x��yʱ��}\end{array}\right.$����ô�Ƶ�QΪ��P�ġ������㡱���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com