【题目】已知下列命题：
①若a＞0，b＞0，则a+b＞0；
②若a2=b2，则a=b；
③线段垂直平分线上的点到线段两端点距离相等；
④平行四边形的对角线互相平分
其中原命题与逆命题均为真命题的是（ ）
A. ①③ B. ②④ C. ③④ D. ②③
阅读快车系列答案科目：初中数学 来源： 题型：
【题目】已知：如图，AB是⊙O的直径，BC是弦，∠B=30°，延长BA到D，使∠BDC=30°．
(1)求证：DC是⊙O的切线；
(2)若AB=2，求DC的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在一笔直的海岸线上有A，B两个观测站，A观测站在B观测站的正东方向，有一艘小船在点P处，从A处测得小船在北偏西60°方向，从B处测得小船在北偏东45°的方向，点P到点B的距离是3
千米．（注：结果有根号的保留根号）
（1）求A，B两观测站之间的距离；
（2）小船从点P处沿射线AP的方向以
千米/时的速度进行沿途考察，航行一段时间后到达点C处，此时，从B测得小船在北偏西15°方向，求小船沿途考察的时间．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】我们把两条中线互相垂直的三角形称为“中垂三角形”，例如图1，图2，图3中，AF，BE是△ABC的中线，AF⊥BE，垂足为P，像△ABC这样的三角形均为“中垂三角形”，设BC=a，AC﹣b，AB=c．
【特例探索】
（1）如图1，当∠ABE=45°，c=2
时，a= ，b= ；如图2，当∠ABE=30°，c=4时，a= ，b= ；
【归纳证明】
（2）请你观察（1）中的计算结果，猜想a2，b2，c2三者之间的关系，用等式表示出来，请利用图3证明你发现的关系式；
【拓展应用】
（3）如图4，在ABCD中，点E，F，G分别是AD，BC，CD的中点，BE⊥EG，AD=2
，AB=3．求AF的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知△ABC是等边三角形，点D、E分别在边BC、AC上，且CD=CE，连接DE并延长至点F，使EF=AE，连接AF，CF，连接BE并延长交CF于点G．下列结论：
①△ABE≌△ACF；②BC=DF；③S△ABC=S△ACF+S△DCF；④若BD=2DC，则GF=2EG．其中正确的结论是 ．（填写所有正确结论的序号）
查看答案和解析>>
科目：初中数学 来源： 题型：
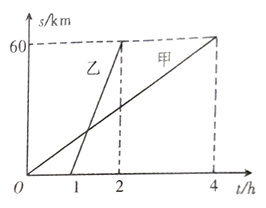
【题目】
两地相距
，甲、乙二人分别骑自行车和摩托车沿相同路线匀速行驶，由
地到达
地．他们行驶的路程
与甲出发后的时间
之间的函数图像如图所示．
（1）乙比甲晚出发几小时？乙比甲早到几小时？
（2）分别写出甲、乙行驶的路程与甲出发后的时间的函数关系式(不写自变量的取值范围)．
（3）乙在甲出发后几小时追上甲？追上甲的地点离地有多远？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，EF∥AD，∠1＝∠2，∠BAC＝70°．将求∠AGD的过程填写完整．
∵EF∥AD，（ ）
∴∠2＝ ．（两直线平行，同位角相等）
又∵∠1＝∠2，（ ）
∴∠1＝∠3．（ ）
∴AB∥DG．（ ）
∴∠BAC+ ＝180°（ ）
又∵∠BAC＝70°，（ ）
∴∠AGD＝ ．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
