【题目】如图，在△ ABC中，∠ ABC、∠ ACB的平分线交于点O。
(1)若∠ABC=40°，∠ ACB=50°，则∠BOC=_______
(2)若∠ABC+∠ ACB=lO0°，则∠BOC=________
(3)若∠A=70°，则∠BOC=_________
(4)若∠BOC=140°，则∠A=________
(5)你能发现∠ BOC与∠ A之间有什么数量关系吗?写出并说明理由。
【答案】(1)、135°；(2)、130°；(3)、125°；(4)、100°；(5)、∠BOC=90°+0.5∠A
【解析】
试题分析：根据角平分线的性质以及三角形内角和定理得出∠OBC和∠OCB与∠A之间的关系，然后根据△BOC的内角和定理得出∠BOC与∠A的关系.
试题解析：(1)135° (2)130° (3)125° (4)100°
(5)、BO平分∠ABC, CO平分∠ABC
∴∠OBC=0.5∠ABC ∠OCB=0.5∠ACB
∴∠OBC+∠OCB=0.5∠ABC+0.5∠ACB=
0.5(180-∠A)=90-0.5∠A
∴∠O=180-(∠OBC+∠OCB)=180-(90-0.5∠A)=90°+0.5∠A
举一反三期末百分冲刺卷系列答案科目：初中数学 来源： 题型：
【题目】某车间有16名工人，每人每天可加工甲种零件5个或乙种零件4个．在这16名工人中，一部分人加工甲种零件，其余的加工乙种零件．已知每加工一个甲种零件可获利16元，每加工一个乙种零件可获利24元．若此车间一共获利1 440元，求这一天有几名工人加工甲种零件．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系中，对于点P(a，b)和点Q(a，b′)，给出如下定义：
若
，则称点Q为点P的限变点．例如：点(2，3)的限变点的坐标是(2，3)，点(－2，5)的限变点的坐标是(－2，－5)．
（1）①点(
，1)的限变点的坐标是 ；
②在点A(－2，－1)，B(－1，2)中有一个点是函数y=
图象上某一个点的限变点，这个点是 ；
（2）若点P在函数y=－x＋3(－2≤x≤k，k＞－2)的图象上，其限变点Q的纵坐标b′的取值范围是－5≤b′≤2，求k的取值范围；
（3）若点P在关于x的二次函数y= x2－2tx＋t2＋t的图象上，其限变点Q的纵坐标b′的取值范围是b′≥m或b′＜n，其中m＞n．令s=m－n，求s关于t的函数解析式并直接写出s的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：如图，平行四边形ABCD的对角线相交于点O，点E在边BC的延长线上，且OE＝OB，联结DE．
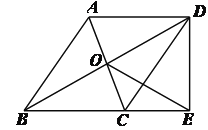
(1)求证：DE⊥BE；
(2)如果OE⊥CD，求证：BD 
CE＝CD DE．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com