练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    13．如图，在△ABC中，∠ACB=90°，将△ACD沿CD折叠，使点A恰好落在BC边上的点E处．若∠B=25°，则∠BDE=40度．

    分析 根据三角形内角和定理求出∠B的度数，根据翻折变换的性质求出∠BCD的度数，根据三角形内角和定理求出∠BDC．

    解答 解：∵将△ACD沿CD折叠，使点A恰好落在BC边上的点E处，
    ∴∠CED=∠A，
    ∵∠ACB=90°，∠B=25°，
    ∴∠A=65°，
    ∴∠CED=65°，
    ∴∠BDE=65°-25°=40°；
    故答案为：40．

    点评 本题考查的是翻折变换和三角形内角和定理，理解翻折变换的性质、熟记三角形内角和等于180°是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

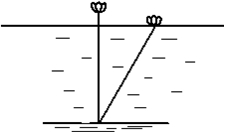    3．在印度数学家拜•什迦罗的著作中，记载了一个有趣的“荷花问题”：
    平平湖水清可鉴，水上一尺生红莲；出泥不染亭亭立，忽被强风吹一边；渔人观看忙向前，花离原位五尺远；能算诸君请解题，湖水深浅知几何？请你用学过的数学知识回答这个问题．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    4．已知抛物线y=x2+bx-3，请你确定一个b的值，使该抛物线与x轴的一个交点在（1，0）和（3，0）之间，你确定的b的值是-1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．已知点P是直线y=（2m+1）x+4m+4（m是常数）上一点，试探究当m取何值时，线段PO≥2$\sqrt{2}$（画图并写出解题思路）

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    8．计算（a2）3正确的是（　　）
    A．a8B．a6C．a5D．a2

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．已知解方程$\frac{4x}{4-{x}^{2}}+1=\frac{k-{k}^{2}}{x-2}+\frac{1}{x+2}$时，不会产生增根，求实数k的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

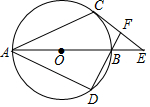    5．如图，AB为⊙O的直径，AC、AD为⊙O的弦，$\widehat{BC}$=$\widehat{BD}$，过C作⊙O的切线交AB的延长线于E，DB的延长线交CE于F，若⊙O的半径为2，∠E=45°，则CF的长为4-2$\sqrt{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    2．已知一次函数y=kx+5和y=k′x+1，假设k＞0且k′＜0，则这两个一次函数的图象的交点在（　　）
    A．第一象限B．第二象限C．第三象限D．第四象限

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    3．如图，平行四边形ABCO中，AO=1，AB=3，点C在x轴的负半轴上，将平行四边形ABCO绕点A逆时针旋转得到平行四边形ADEF，AD经过点O，点F恰好落在x轴上，若点D在反比例函数y=$\frac{k}{x}$的图象上，则k的值为$\sqrt{3}$．

    查看答案和解析>>

    同步练习册答案