
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{6}÷(\sqrt{3}-\sqrt{2})=\sqrt{2}-\sqrt{3}$ | B. | $\sqrt{(-9)×(-25)}=\sqrt{-9}×\sqrt{-25}=(-3)×(-5)=15$ | ||
| C. | $\sqrt{2}(\sqrt{3}+\sqrt{2})=\sqrt{10}$ | D. | $\sqrt{{{13}^2}-{{12}^2}}=\sqrt{(13+12)×(13-12)}=5$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
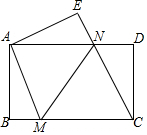 如图,将一张矩形纸片ABCD沿直线MN折叠,使点C落住点A处,点D落在点E处,直线MN交BC于点M,交AD于点N
如图,将一张矩形纸片ABCD沿直线MN折叠,使点C落住点A处,点D落在点E处,直线MN交BC于点M,交AD于点N查看答案和解析>>
科目:初中数学 来源: 题型:解答题
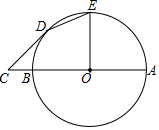 已知AB为⊙O的直径,C为AB延长线上一点,CD切⊙O于点D,CD=4,BC=2
已知AB为⊙O的直径,C为AB延长线上一点,CD切⊙O于点D,CD=4,BC=2查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,小红用一张长方形纸片ABCD进行折纸,已知纸片宽AB为8cm,长BC为10cm.当小红折叠时,顶点D落在BC边上的点F处(折痕为AE),求此时EC的长?
如图,小红用一张长方形纸片ABCD进行折纸,已知纸片宽AB为8cm,长BC为10cm.当小红折叠时,顶点D落在BC边上的点F处(折痕为AE),求此时EC的长?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
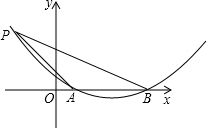 如图,已知抛物线y=ax2+bx+c与x轴交于A、B两点,AB=4,P是抛物线上一点,它的横坐标为-2,∠PAO=45°,cot∠PBO=$\frac{7}{3}$,求:
如图,已知抛物线y=ax2+bx+c与x轴交于A、B两点,AB=4,P是抛物线上一点,它的横坐标为-2,∠PAO=45°,cot∠PBO=$\frac{7}{3}$,求:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
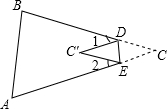 如图,将△ABC纸片的一角折叠,使点C落在△ABC内一点C′上,若∠1=30°,∠2=36°,则∠C的度数是( )
如图,将△ABC纸片的一角折叠,使点C落在△ABC内一点C′上,若∠1=30°,∠2=36°,则∠C的度数是( )| A. | 33° | B. | 34° | C. | 31° | D. | 32° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
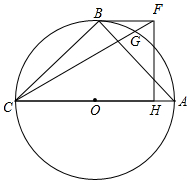 如图,△ABC内接于⊙O,AC是直径,BC=BA,在∠ACB的内部作∠ACF=30°,且CF=CA,过点F作FH⊥AC于点H,连接BF.
如图,△ABC内接于⊙O,AC是直径,BC=BA,在∠ACB的内部作∠ACF=30°,且CF=CA,过点F作FH⊥AC于点H,连接BF.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com