
【题目】如图1,△ABC中,AB=AC,∠BAC=90°,CD平分∠ACB,BE⊥CD,垂足E在CD的延长线上.请解答下列问题:
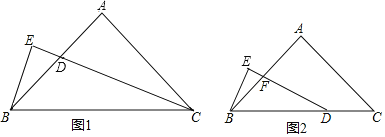
(1)图中与∠DBE相等的角有: ;
(2)直接写出BE和CD的数量关系;
(3)若△ABC的形状、大小不变,直角三角形BEC变为图2中直角三角形BED,∠E=90°,且∠EDB=![]() ∠C,DE与AB相交于点F.试探究线段BE与FD的数量关系,并证明你的结论.
∠C,DE与AB相交于点F.试探究线段BE与FD的数量关系,并证明你的结论.
【答案】(1)∠ACE和∠BCD;
(2)BE=![]() CD;
CD;
(3)BE=![]() DF,证明见解析
DF,证明见解析
【解析】
(1)根据三角形内角和定理得到∠DBE=∠ACE,根据角平分线的定义得到∠BCD=∠ACE,得到答案;
(2)延长BE交CA延长线于F,证明△CEF≌△CEB,得到FE=BE,证明△ACD≌△ABF,得到CD=BF,证明结论;
(3)过点D作DG∥CA,交BE的延长线于点G,与AE相交于H,分别证明△BGH≌△DFH、△BDE≌△GDE,根据全等三角形的性质解答即可.
解:(1)∵BE⊥CD,
∴∠E=90°,
∴∠E=∠BAC,又∠EDB=∠ADC,
∴∠DBE=∠ACE,
∵CD平分∠ACB,
∴∠BCD=∠ACE,
∴∠DBE=∠BCD,
故答案为:∠ACE和∠BCD;
(2)延长BE交CA延长线于F,
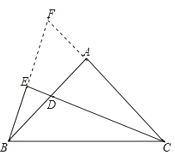
∵CD平分∠ACB,
∴∠FCE=∠BCE,
在△CEF和△CEB中,
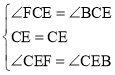 ,
,
∴△CEF≌△CEB(ASA),
∴FE=BE,
在△ACD和△ABF中,
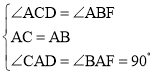 ,
,
∴△ACD≌△ABF(ASA),
∴CD=BF,
∴BE=![]() CD;
CD;
(3)BE=![]() DF
DF
证明:过点D作DG∥CA,交BE的延长线于点G,与AE相交于H,
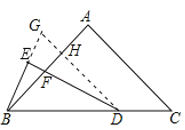
∵DG∥AC,
∴∠GDB=∠C,∠BHD=∠A=90°,
∵∠EDB=![]() ∠C,
∠C,
∴∠EDB=∠EDG=![]() ∠C,
∠C,
∵BE⊥ED,
∴∠BED=90°,
∴∠BED=∠BHD,
∵∠EFB=∠HFD,
∴∠EBF=∠HDF,
∵AB=AC,∠BAC=90°,
∴∠C=∠ABC=45°,
∵GD∥AC,
∴∠GDB=∠C=45°,
∴∠GDB=∠ABC=45°,
∴BH=DH,
在△BGH和△DFH中,
 ,
,
∴△BGH≌△DFH(ASA)
∴BG=DF,
∵在△BDE和△GDE中,
 ,
,
∴△BDE≌△GDE(ASA)
∴BE=EG,
∴BE=![]() .
.


 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:初中数学 来源: 题型:
【题目】利用我们学过的知识,可以得出下面这个优美的等式:
![]() ;该等式从左到右的变形,不仅保持了结构的对称性,还体现了数学的和谐、简洁美.
;该等式从左到右的变形,不仅保持了结构的对称性,还体现了数学的和谐、简洁美.
⑴.请你证明这个等式;
⑵.如果![]() ,请你求出
,请你求出 ![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,已知平面内一点![]() 与一直线
与一直线![]() ,如果过点
,如果过点![]() 作直线
作直线![]() ,垂足为
,垂足为![]() ,那么垂足
,那么垂足![]() 叫做点
叫做点![]() 在直线
在直线![]() 上的射影;如果线段
上的射影;如果线段![]() 的两个端点
的两个端点![]() 和
和![]() 在直线
在直线![]() 上的射影分别为点
上的射影分别为点![]() 和
和![]() ,那么线段
,那么线段![]() 叫做线段
叫做线段![]() 在直线
在直线![]() 上的射影.
上的射影.
如图①,已知平面内一点![]() 与一直线
与一直线![]() ,如果过点
,如果过点![]() 作直线
作直线![]() ,垂足为
,垂足为![]() ,那么垂足
,那么垂足![]() 叫做点
叫做点![]() 在直线
在直线![]() 上的射影;如果线段
上的射影;如果线段![]() 的两个端点
的两个端点![]() 和
和![]() 在直线
在直线![]() 上的射影分别为点
上的射影分别为点![]() 和
和![]() ,那么线段
,那么线段![]() 叫做线段
叫做线段![]() 在直线
在直线![]() 上的射影.
上的射影.
![]() 如图②,
如图②,![]() 、
、![]() 为线段
为线段![]() 外两点,
外两点,![]() ,
,![]() ,垂足分别为
,垂足分别为![]() 、
、![]() .
.
则![]() 点在
点在![]() 上的射影是________点,
上的射影是________点,![]() 点在
点在![]() 上的射影是________点,
上的射影是________点,
线段![]() 在
在![]() 上的射影是________,线段
上的射影是________,线段![]() 在
在![]() 上的射影是________;
上的射影是________;
![]() 根据射影的概念,说明:直角三角形斜边上的高是两条直角边在斜边上射影的比例中项.(要求:画出图形,写出说理过程.)
根据射影的概念,说明:直角三角形斜边上的高是两条直角边在斜边上射影的比例中项.(要求:画出图形,写出说理过程.)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小玲和弟弟小东分别从家和图书馆同时当发,沿同一条路相向而行,小玲开始跑步,中途改为步行,到达图书馆恰好用30min.小东骑自行车以300m/min的速度直接回家,两人离家的路程y(m)与各自离开出发地的时间x(min)之间的函数函象如图所示.
(1)家与图书馆之间的路程为 m,小东从图书馆到家所用的时间为 .
(2)求小玲步行时y与x之间的函数关系式
(3)求两人相遇的时间.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】ΔABC、ΔCDE都是等边三角形,AD、BE相交于点O,点M、点N分别是线段AD、BE的中点.
(1)证明: AD=BE.(2)求∠DOE的角度。(3)证明:ΔMNC是等边三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
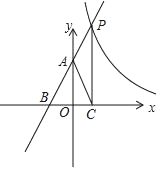
【题目】已知,如图所示直线y=kx+2(k≠0)与反比例函数y=![]() (m≠0)分别交于点P,与y轴、x轴分别交于点A和点B,且cos∠ABO=
(m≠0)分别交于点P,与y轴、x轴分别交于点A和点B,且cos∠ABO=![]() ,过P点作x轴的垂线交于点C,连接AC,
,过P点作x轴的垂线交于点C,连接AC,
(1)求一次函数的解析式.
(2)若AC是△PCB的中线,求反比例函数的关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,ACB和DCE都是等腰直角三角形,∠ACB=∠DCE=90![]() ,连接AE、BD交于点O. AE与DC交于点M,BD与AC交于点N.
,连接AE、BD交于点O. AE与DC交于点M,BD与AC交于点N.
(1)如图①,求证:AE=BD;
(2)如图②,若AC=DC,在不添加任何辅助线的情况下,请直接写出图②中四对全等的直角三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,AC是弦,直线EF经过点C,AD⊥EF于点D,∠DAC=∠BAC.

(1)求证:EF是⊙O的切线;
(2)求证:AC2=AD·AB;
(3)若⊙O的半径为2,∠ACD=300,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),在等边三角形![]() 中,
中,![]() 是
是![]() 边上的动点,以
边上的动点,以![]() 为一边,向上作等边三角形
为一边,向上作等边三角形![]() ,连接
,连接![]() .
.
(1)![]() 和
和![]() 全等吗?请说明理由;
全等吗?请说明理由;
(2)试说明:![]() ;
;
(3)如图(2),将动点![]() 运动到边
运动到边![]() 的延长线上,所作三角形
的延长线上,所作三角形![]() 仍为等边三角形,请问是否仍有
仍为等边三角形,请问是否仍有![]() ?请说明理由.
?请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com