
【题目】利用我们学过的知识,可以得出下面这个优美的等式:
![]() ;该等式从左到右的变形,不仅保持了结构的对称性,还体现了数学的和谐、简洁美.
;该等式从左到右的变形,不仅保持了结构的对称性,还体现了数学的和谐、简洁美.
⑴.请你证明这个等式;
⑵.如果![]() ,请你求出
,请你求出 ![]() 的值.
的值.
科目:初中数学 来源: 题型:
【题目】任丘市举办一场中学生乒乓球比赛,比赛的费用y(元)包括两部分:一部分是租用比赛场地等固定不变的费用b(元),另一部分费用与参加比赛的人数(x)人成正比.当x=20时,y=1600;当x=30时,y=2000.
(1)求y与x之间的函数关系式;
(2)如果承办此次比赛的组委会共筹集;经费6350元,那么这次比赛最多可邀请多少名运动员参赛?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】等腰Rt△ACB,∠ACB=90°,AC=BC,点A、C分别在x轴、y轴的正半轴上.

(1)如图1,求证:∠BCO=∠CAO
(2)如图2,若OA=5,OC=2,求B点的坐标
(3)如图3,点C(0,3),Q、A两点均在x轴上,且S△CQA=18.分别以AC、CQ为腰在第一、第二象限作等腰Rt△CAN、等腰Rt△QCM,连接MN交y轴于P点,OP的长度是否发生改变?若不变,求出OP的值;若变化,求OP的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠BOC=9°,点A在OB上,且OA=1,按下列要求画图:以A为圆心,1为半径向右画弧交OC于点A1,得第1条线段AA1;再以A1为圆心,1为半径向右画弧交OB于点A2,得第2条线段A1A2;再以A2为圆心,1为半径向右画弧交OC于点A3,得第3条线段A2A3…这样画下去,直到得第n条线段,之后就不能再画出符合要求的线段了,则n=( )
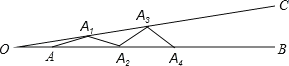
A. 10B. 9C. 8D. 7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)a3aa2﹣9a2a4
(2)﹣m2(﹣m2)4(﹣m)3
(3)(﹣8)2018×(﹣0.125)2017
(4)(﹣![]() a2b﹣2ab2+
a2b﹣2ab2+![]() )(﹣9a)
)(﹣9a)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是正方形,△ADF旋转一定角度后得到△ABE,且点E在线段AD上,若AF=4,∠F=60°.
(1)指出旋转中心和旋转角度;
(2)求DE的长度和∠EBD的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC中,AB=AC,∠BAC=90°,CD平分∠ACB,BE⊥CD,垂足E在CD的延长线上.请解答下列问题:
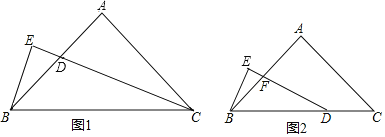
(1)图中与∠DBE相等的角有: ;
(2)直接写出BE和CD的数量关系;
(3)若△ABC的形状、大小不变,直角三角形BEC变为图2中直角三角形BED,∠E=90°,且∠EDB=![]() ∠C,DE与AB相交于点F.试探究线段BE与FD的数量关系,并证明你的结论.
∠C,DE与AB相交于点F.试探究线段BE与FD的数量关系,并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com