
【题目】如图,四边形ABCD是正方形,△ADF旋转一定角度后得到△ABE,且点E在线段AD上,若AF=4,∠F=60°.
(1)指出旋转中心和旋转角度;
(2)求DE的长度和∠EBD的度数.

【答案】(1) 90°;(2) 15°.
【解析】
试题(1)由于△ADF旋转一定角度后得到△ABE,根据旋转的性质得到旋转中心为点A,∠DAB等于旋转角,于是得到旋转角为90°;(2)根据旋转的性质得到AE=AF=4,∠AEB=∠F=60°,则∠ABE=90°﹣60°=30°,解直角三角形得到AD=4![]() ,∠ABD=45°,所以DE=4
,∠ABD=45°,所以DE=4![]() ﹣4,然后利用∠EBD=∠ABD﹣∠ABE计算即可.
﹣4,然后利用∠EBD=∠ABD﹣∠ABE计算即可.
试题解析:(1)∵△ADF旋转一定角度后得到△ABE,
∴旋转中心为点A,∠DAB等于旋转角,
∴旋转角为90°;
(2)∵△ADF以点A为旋转轴心,顺时针旋转90°后得到△ABE,
∴AE=AF=4,∠AEB=∠F=60°,
∴∠ABE=90°﹣60°=30°,
∵四边形ABCD为正方形,
∴AD=AB=4![]() ,∠ABD=45°,
,∠ABD=45°,
∴DE=4![]() ﹣4,
﹣4,
∠EBD=∠ABD﹣∠ABE=15°.


科目:初中数学 来源: 题型:
【题目】如图所示,现有边长为1,a(a>1)的一张矩形纸片ABCD,把这个矩形按要求分割,画出分割线,并在相应的位置上写出a的值.
(1)把这个矩形分成两个全等的小矩形,且分成的两个矩形与原矩形相似.
(2)把这个和矩形分成三个矩形,且每一个矩形都与原矩形相似,给出两种不同的分割.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】利用我们学过的知识,可以得出下面这个优美的等式:
![]() ;该等式从左到右的变形,不仅保持了结构的对称性,还体现了数学的和谐、简洁美.
;该等式从左到右的变形,不仅保持了结构的对称性,还体现了数学的和谐、简洁美.
⑴.请你证明这个等式;
⑵.如果![]() ,请你求出
,请你求出 ![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC, 点M在△ABC内,点P在线段MC上,∠ABP=2∠ACM.

(1)若∠PBC=10°,∠BAC=80°,求∠MPB的值
(2)若点M在底边BC的中线上,且BP=AC,试探究∠A与∠ABP之间的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题:
现有甲、乙两种机器加工零件,甲种机器比乙种机器每小时多加工30个,甲种机器加工900个零件所用时间与乙种机器加工600个零件所用时间相等,求两种机器每小时各加工多少个零件?
查看答案和解析>>
科目:初中数学 来源: 题型:
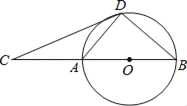
【题目】如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
(1)求证:CD是⊙O的切线;
(2)若BC=6,tan∠CDA=![]() ,求CD的长.
,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,已知平面内一点![]() 与一直线
与一直线![]() ,如果过点
,如果过点![]() 作直线
作直线![]() ,垂足为
,垂足为![]() ,那么垂足
,那么垂足![]() 叫做点
叫做点![]() 在直线
在直线![]() 上的射影;如果线段
上的射影;如果线段![]() 的两个端点
的两个端点![]() 和
和![]() 在直线
在直线![]() 上的射影分别为点
上的射影分别为点![]() 和
和![]() ,那么线段
,那么线段![]() 叫做线段
叫做线段![]() 在直线
在直线![]() 上的射影.
上的射影.
如图①,已知平面内一点![]() 与一直线
与一直线![]() ,如果过点
,如果过点![]() 作直线
作直线![]() ,垂足为
,垂足为![]() ,那么垂足
,那么垂足![]() 叫做点
叫做点![]() 在直线
在直线![]() 上的射影;如果线段
上的射影;如果线段![]() 的两个端点
的两个端点![]() 和
和![]() 在直线
在直线![]() 上的射影分别为点
上的射影分别为点![]() 和
和![]() ,那么线段
,那么线段![]() 叫做线段
叫做线段![]() 在直线
在直线![]() 上的射影.
上的射影.
![]() 如图②,
如图②,![]() 、
、![]() 为线段
为线段![]() 外两点,
外两点,![]() ,
,![]() ,垂足分别为
,垂足分别为![]() 、
、![]() .
.
则![]() 点在
点在![]() 上的射影是________点,
上的射影是________点,![]() 点在
点在![]() 上的射影是________点,
上的射影是________点,
线段![]() 在
在![]() 上的射影是________,线段
上的射影是________,线段![]() 在
在![]() 上的射影是________;
上的射影是________;
![]() 根据射影的概念,说明:直角三角形斜边上的高是两条直角边在斜边上射影的比例中项.(要求:画出图形,写出说理过程.)
根据射影的概念,说明:直角三角形斜边上的高是两条直角边在斜边上射影的比例中项.(要求:画出图形,写出说理过程.)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小玲和弟弟小东分别从家和图书馆同时当发,沿同一条路相向而行,小玲开始跑步,中途改为步行,到达图书馆恰好用30min.小东骑自行车以300m/min的速度直接回家,两人离家的路程y(m)与各自离开出发地的时间x(min)之间的函数函象如图所示.
(1)家与图书馆之间的路程为 m,小东从图书馆到家所用的时间为 .
(2)求小玲步行时y与x之间的函数关系式
(3)求两人相遇的时间.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,AC是弦,直线EF经过点C,AD⊥EF于点D,∠DAC=∠BAC.

(1)求证:EF是⊙O的切线;
(2)求证:AC2=AD·AB;
(3)若⊙O的半径为2,∠ACD=300,求图中阴影部分的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com