
【题目】如图,已知![]() ,
,![]() ,BE与CF交于点D,则对于下列结论:
,BE与CF交于点D,则对于下列结论:![]() ≌
≌![]() ;
;![]() ≌
≌![]() ;
;![]() ≌
≌![]() ;
;![]() 在
在![]() 的平分线上
的平分线上![]() 其中正确的是( )
其中正确的是( )

A. ①②③ B. ②③④ C. ①③④ D. ①②③④
【答案】D
【解析】
(1)由AB=AC易得∠ABC=∠ACB,结合FB=EC,BC=CB即可证得△BCE≌△CBF;(2)由AB=AC,EC=FB易得AF=AE,结合∠A=∠A即可证得△ABE≌△ACF;(3)由△ABE≌△ACF可得∠FBD=∠ECD,结合∠BDF=∠CDE,FB=EC即可证得△BDF≌△CDE;(4)连接AD,由△BDF≌△CDE可得DF=DE,结合AF=AE,AD=AD可得△ADF≌△ADE,由此可得∠DAF=∠DAE,从而说明AD平分∠BAC;综上即可得到4个结论都成立,由此即可知该选D.
(1)∵AB=AC,
∴∠ABC=∠ACB,
又∵FB=EC,BC=CB,
∴△BCE≌△CBF(SAS),即结论①正确;
(2)∵AB=AC,EC=FB,
∴AB-FB=AC-EC,即AF=AE,
又∵∠A=∠A,
∴△ABE≌△ACF(SAS),即结论②正确;
(3)∵△ABE≌△ACF,
∴∠FBD=∠ECD,
又∵∠BDF=∠CDE,FB=EC,
∴△BDF≌△CDE(AAS),即结论③正确;
(4)连接AD,∵△BDF≌△CDE,
∴DF=DE,
又∵AF=AE,AD=AD,
∴△ADF≌△ADE(SSS),
∴∠DAF=∠DAE,
∴AD平分∠BAC,即点D在∠BAC的角平分线上,即结论④正确.
综上所述,题中4个结论都是正确的.
故选D.


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:初中数学 来源: 题型:
【题目】如图,从左边第一个格子开始向右数,在每个小格子中都填入一个整数,使得其中任意三个相邻格子中所填整数之和都相等.
6 | a | b | x | -2 | 1 | … |
(1)可求得x=______,第2016个格子中的数为______;
(2)判断:前m个格子中所填整数之和是否可能为2016?若能,求出m的值,若不可能,请说明理由;
(3)如果x,y为前3格子中的任意两个数,那么所有的|x-y|的和可以通过计算|6-a|+|a-6|+|a-b|+|b-a|+|6-b|+|b-6|得到.若x,y为前20格子中的任意两个数,则所有的|a-b|的和为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,对称轴为直线x= ![]() 的抛物线经过点A(6,0)和B(0,﹣4).
的抛物线经过点A(6,0)和B(0,﹣4). 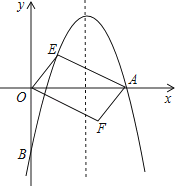
(1)求抛物线解析式及顶点坐标;
(2)设点E(x,y)是抛物线上一动点,且位于第一象限,四边形OEAF是以OA为对角线的平行四边形,求平行四边形OEAF的面积S与x之间的函数关系式;
(3)当(2)中的平行四边形OEAF的面积为24时,请判断平行四边形OEAF是否为菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点A、B的坐标分别为(8,0)、(0,2 ![]() ),C是AB的中点,过点C作y轴的垂线,垂足为D,动点P从点D出发,沿DC向点C匀速运动,过点P作x轴的垂线,垂足为E,连接BP、EC.当BP所在直线与EC所在直线第一次垂直时,点P的坐标为
),C是AB的中点,过点C作y轴的垂线,垂足为D,动点P从点D出发,沿DC向点C匀速运动,过点P作x轴的垂线,垂足为E,连接BP、EC.当BP所在直线与EC所在直线第一次垂直时,点P的坐标为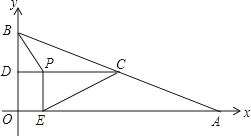
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OABC是一张放在平面直角坐标系中的长方形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=10 ,OC=8.在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处.
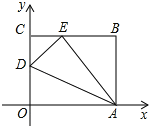
(1)求CE和OD的长;
(2)求直线DE的表达式;
(3)直线y=kx+b与DE平行,当它与矩形OABC有公共点时,直接写出b的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() ,则在下列条件:①∠C=∠D ②AC=AD ③∠CBA=∠DBA ④BC=BD中任选一个能判定△ABC≌△ABD的是( )
,则在下列条件:①∠C=∠D ②AC=AD ③∠CBA=∠DBA ④BC=BD中任选一个能判定△ABC≌△ABD的是( )

A. ①②③④ B. ②③④ C. ①③④ D. ①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(阅读材料)“九宫图”源于我国古代夏禹时期的“洛书”![]() 图1所示
图1所示![]() ,是世界上最早的矩阵,又称“幻方”,用今天的数学符号翻译出来,“洛书”就是一个三阶“幻方”
,是世界上最早的矩阵,又称“幻方”,用今天的数学符号翻译出来,“洛书”就是一个三阶“幻方”![]() 图2所示
图2所示![]() .
.
(规律总结)观察图1、图2,根据“九宫图”中各数字之间的关系,我们可以总结出“幻方”需要满足的条件是______;若图3,是一个“幻方”,则![]() ______.
______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面题目的解题过程,并回答问题.
若![]() ,求x2+y2的值.
,求x2+y2的值.
解:设![]() ,则原式可化为a2-8a+16=0,即(a-4)2=0,所以a=4.
,则原式可化为a2-8a+16=0,即(a-4)2=0,所以a=4.
由(x2+y2)2=4,得x2+y2=±2.
(1)错误的原因是___________________________________
(2)本题正确的结论为_________________________________
(3)设“![]() ”的方法叫做换元法,它能起到化繁为简的目的.请用“换元法”把(x+y)2-14(x+y)+49因式分解.
”的方法叫做换元法,它能起到化繁为简的目的.请用“换元法”把(x+y)2-14(x+y)+49因式分解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行于y轴的直尺(一部分)与双曲线y= ![]() (k≠0)(x>0)相交于点A、C,与x轴相交于点B、D,连接AC.已知点A、B的刻度分别为5,2(单位:cm),直尺的宽度为2cm,OB=2cm.
(k≠0)(x>0)相交于点A、C,与x轴相交于点B、D,连接AC.已知点A、B的刻度分别为5,2(单位:cm),直尺的宽度为2cm,OB=2cm.
(1)求k的值;
(2)求经过A、C两点的直线的解析式;
(3)连接OA、OC,求△OAC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com