Question

【题目】如图，对称轴为直线x= 的抛物线经过点A（6，0）和B（0，﹣4）．
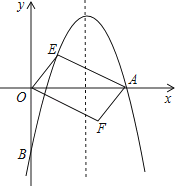
（1）求抛物线解析式及顶点坐标；
（2）设点E（x，y）是抛物线上一动点，且位于第一象限，四边形OEAF是以OA为对角线的平行四边形，求平行四边形OEAF的面积S与x之间的函数关系式；
（3）当（2）中的平行四边形OEAF的面积为24时，请判断平行四边形OEAF是否为菱形．

Answer 1

【答案】
（1）

解：设抛物线的解析式为y=ax2+bx+c，

将A、B点的坐标代入函数解析式，得

，

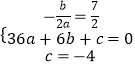解得 ，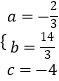

抛物线的解析式为y=﹣ x2+ x﹣4，

配方，得

y=﹣ （x﹣ ）2+ ，

顶点坐标为（ ， ）；

（2）

解：E点坐标为（x，﹣ x2+ x﹣4），

S=2× OAyE=3（﹣ x2+ x﹣4）

即S=﹣2x2+14x﹣12；

（3）

解：平行四边形OEAF的面积为24时，平行四边形OEAF不能为菱形，理由如下：

当平行四边形OEAF的面积为24时，即

﹣2x2+14x﹣12=24，

化简，得

x2﹣7x+18=0，

△=b2﹣4ac=（﹣7）2﹣4×18=﹣23＜0，

方程无解，

E点不存在，

平行四边形OEAF的面积为24时，平行四边形OEAF不能为菱形

【解析】（1）根据对称轴、A、B点的坐标，可得方程，根据解方程，可得答案；
　　　　（2）根据平行四边形的面积公式，可得函数解析式；
　　　　（3）根据函数值，可得E点坐标，根据菱形的判定，可得答案．本题考查了二次函数综合题，利用待定系数法求函数解析式，配方法求函数的顶点坐标；利用平行四边形性质是解题关键；利用方程的判别式是解题关键．