
【题目】如图所示,△ABC是等边三角形,点D为AB上一点,现将△ABC沿EF折叠,使得顶点A与D点重合,且FD⊥BC,则 ![]() 的值等于( )
的值等于( ) 
A.![]()
B.![]()
C.![]()
D.![]()
【答案】D
【解析】解:如图,过点E作EG⊥BC于点G, 
由题意知AE=DE、AF=DF、∠A=∠EDF=60°,
设EG=x,
∵FD⊥BC,
∴∠FDC=90°,
∴∠EDG=30°,
则AE=DE=2EG=2x,DG= ![]() =
= ![]() x,
x,
∴BE= ![]() =
= ![]() =
= ![]() x,BG=
x,BG= ![]() =
= ![]() =
= ![]() x,
x,
∴BC=AB=AE+BE=2x+ ![]() x=
x= ![]() x,
x,
∵CD=BC﹣BD= ![]() x﹣(
x﹣( ![]() x+
x+ ![]() x)=
x)= ![]() x,
x,
∴AF=DF=CDtanC= ![]() x
x ![]() =(2
=(2 ![]() ﹣2)x,
﹣2)x,
∴ ![]() =
= ![]() =
= ![]() ,
,
故选:D.
【考点精析】本题主要考查了等边三角形的性质和翻折变换(折叠问题)的相关知识点,需要掌握等边三角形的三个角都相等并且每个角都是60°;折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等才能正确解答此题.


 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,BE、DF分别是∠ABC、∠ADC的平分线,且与对角线AC分别相交于点E、F. 
(1)求证:AE=CF;
(2)连结ED、FB,判断四边形BEDF是否是平行四边形,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠BAC=54°,以AB为直径的⊙O分别交AC,BC于点D,E,过点B作⊙O的切线,交AC的延长线于点F. 
(1)求证:BE=CE;
(2)求∠CBF的度数;
(3)若AB=6,求 ![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:求1+2+22+23+24+…+22019的值.
解:设S=1+2+22+23+24+…+22018+22019,①将等式两边同时乘2,得
2S=2+22+23+24+25+…+22019+22020,②
将②式减去①式,得2S-S=22020-1,
即S=22020-1,
则1+2+22+23+24+…+22019=22020-1.
请你仿照此法计算:
(1)1+2+22+23+24+…+210;
(2)1+3+32+33+34+…+3n(其中n为正整数).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】周末,老师带同学去北京植物园中的一二﹒九运动纪念广场,这里有三座侧面为三角形的纪念亭,挺拔的建筑线条象征青年朝气蓬勃、积极向上的精神.基于纪念亭的几何特征,同学们编拟了如下的数学问题:

如图1,点A,B,C,D在同一条直线上,在四个论断“EA=ED,EF⊥AD,AB=DC,FB=FC”中选择三个作为已知条件,另一个作为结论,构成真命题(补充已知和求证),并进行证明.
已知:如图,点A,B,C,D在同一条直线上, .
求证: .
证明: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数y= ![]() (x>0)的图象经过矩形OABC对角线的交点M,分别与AB、BC相交于点D、E.,则下列结论正确的是(将正确的结论填在横线上).
(x>0)的图象经过矩形OABC对角线的交点M,分别与AB、BC相交于点D、E.,则下列结论正确的是(将正确的结论填在横线上).
①s△OEB=s△ODB , ②BD=4AD,③连接MD,S△ODM=2S△OCE , ④连接ED,则△BED∽△BCA.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据2008~2012年杭州市实现地区生产总值(简称GDP,单位:亿元)统计图所提供的信息,下列判断正确的是( ) 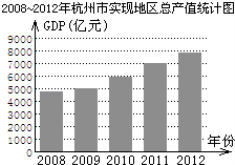
A.2010~2012年杭州市每年GDP增长率相同
B.2012年杭州市的GDP比2008年翻一番
C.2010年杭州市的GDP未达到5500亿元
D.2008~2012年杭州市的GDP逐年增长
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com