
【题目】已知a=﹣(﹣2)2×3,b=|﹣9|+7,c=![]() .
.
(1)求3[a﹣(b+c)]﹣2[b﹣(a﹣2c)]的值.
(2)若A=![]() ×(1﹣3)2,B=|a|﹣b+c,试比较A和B的大小.
×(1﹣3)2,B=|a|﹣b+c,试比较A和B的大小.
(3)如图,已知点D是线段AC的中点,点B是线段DC上的一点,且CB:BD=2:3,若AB=![]() cm,求BC的长.
cm,求BC的长.
![]()
【答案】(1)﹣126;(2)A>B,理由见解析;(3)BC=2cm
【解析】
(1)先求出a、b、c的值,再把式子化简后代入a、b、c的值即可求解;
(2)先求出A的值,再代入a、b、c的值求出B的值即可比较大小;
(3)先求出AB的长度,再根据比例线段列方程解答即可.
解:a=﹣(﹣2)2×3=﹣4×3=﹣12, b=|﹣9|+7=9+7=16,
c=(![]() )×15=﹣
)×15=﹣![]() ,
,
(1)3[a﹣(b+c)]﹣2[b﹣(a﹣2c)]=3a﹣3(b+c)﹣2b+2(a﹣2c)
=3a﹣3b﹣3c﹣2b+2a﹣4c=5a﹣5b﹣7c,
当a=﹣12,b=16,c=﹣2时,
原式=5×(﹣12)﹣5×16﹣7×(﹣2)=﹣60﹣80+14=﹣126;
(2)A=(﹣![]() )2÷(﹣
)2÷(﹣![]() )+(1﹣
)+(1﹣![]() )2×(1﹣3)2
)2×(1﹣3)2
![]()
=![]()
=![]() ;
;
B=|a|﹣b+c=12﹣16+(﹣2)=﹣6,
∴A>B;
(3)AB=![]() .
.
∵CB:BD=2:3,
∴设CB=2x,DB=3x,则DC=CB+DB=5x.
∵点D是线段AC的中点,
∴AD=DC=5x,即AB=8x.
∴8x=8,
∴x=1,
∴BC=2cm.


科目:初中数学 来源: 题型:
【题目】观察下列等式:![]() ,
,![]() ,
,![]() ,则以上三个等式两边分别相加得:
,则以上三个等式两边分别相加得:![]() .
.
![]() 观察发现
观察发现
![]() ______;
______;![]() ______.
______.
![]() 拓展应用
拓展应用
有一个圆,第一次用一条直径将圆周分成两个半圆![]() 如图
如图![]() ,在每个分点标上质数m,记2个数的和为
,在每个分点标上质数m,记2个数的和为![]() ;第二次再将两个半圆周都分成
;第二次再将两个半圆周都分成![]() 圆周
圆周![]() 如图
如图![]() ,在新产生的分点标上相邻的已标的两数之和的
,在新产生的分点标上相邻的已标的两数之和的![]() ,记4个数的和为
,记4个数的和为![]() ;第三次将四个
;第三次将四个![]() 圆周分成
圆周分成![]() 圆周
圆周![]() 如图
如图![]() ,在新产生的分点标上相邻的已标的两数之和的
,在新产生的分点标上相邻的已标的两数之和的![]() ,记8个数的和为
,记8个数的和为![]() ;第四次将八个
;第四次将八个![]() 圆周分成
圆周分成![]() 圆周,在新产生的分点标上相邻的已标的两个数的和的
圆周,在新产生的分点标上相邻的已标的两个数的和的![]() ,记16个数的和为
,记16个数的和为![]() ;
;![]() 如此进行了n次.
如此进行了n次.
![]() ______
______![]() 用含m、n的代数式表示
用含m、n的代数式表示![]() ;
;
![]() 当
当![]() 时,求
时,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某开发公司要生产若干件新产品,需要精加工后,才能投放市场,现有红星和巨星两家加工厂都想加工这批产品,已知红星厂单独加工比巨星厂单独加工这批产品多用20天,红星厂每天可加工16件产品,巨星厂每天可加工24件产品,公司需付给红星厂每天加工费800元,付给巨星厂每天加工费1200元.
![]() 这个公司要加工多少件新产品?
这个公司要加工多少件新产品?
![]() 公司的产品可由一家工厂单独加工完成,也可由两家工厂合作完成,在加工过程中公司需另派一名工程师每天到厂家进行指导,并支付工程师每天10元的午餐补助,请你帮助公司从所有可供选择的方案中,选择一种既省钱又省时的加工方案.
公司的产品可由一家工厂单独加工完成,也可由两家工厂合作完成,在加工过程中公司需另派一名工程师每天到厂家进行指导,并支付工程师每天10元的午餐补助,请你帮助公司从所有可供选择的方案中,选择一种既省钱又省时的加工方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某社区超市第一次用6000元购进甲、乙两种商品,其中乙商品的件数比甲商品件数的![]() 倍多15件,甲、乙两种商品的进价和售价如下表:(注:获利=售价﹣进价)
倍多15件,甲、乙两种商品的进价和售价如下表:(注:获利=售价﹣进价)
甲 | 乙 | |
进价(元/件) | 22 | 30 |
售价(元/件) | 29 | 40 |
(1)该超市购进甲、乙两种商品各多少件?
(2)该超市将第一次购进的甲、乙两种商品全部卖完后一共可获得多少利润?
(3)该超市第二次以第一次的进价又购进甲、乙两种商品,其中甲商品的件数不变,乙商品的件数是第一次的3倍;甲商品按原价销售,乙商品打折销售,第二次两种商品都销售完以后获得的总利润比第一次获得的总利润多180元,求第二次乙商品是按原价打几折销售?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个安装了两个进水管和一个出水管的容器,每分钟的进水量和出水量是两个常数,且两个进水管的进水速度相同.进水管和出水管的进出水速度如图1所示,某时刻开始到6分钟(至少打开一个水管),该容器的水量y(单位:升)与时间x如图2所示.
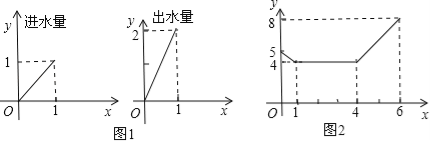
(1)试判断0到1分、1分到4分、4分到6分这三个时间段的进水管和出水管打开的情况.
(2)求4≤x≤6时,y随x变化的函数关系式.
(3)6分钟后,若同时打开两个水管,则10分钟时容器的水量是多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小山岗的斜坡AC的坡角α=45°,在与山脚C距离200米的D处,测得山顶A的仰角为26.6°,小山岗的高AB约为(结果取整数,参考数据:sin26.6°=0.45,cos26.6°=0.89,tan26.6°=0.50)( )
A.164m
B.178m
C.200m
D.1618m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图1,射线OP∥AE,∠AOP的角平分线交射线AE于点B.
(1)若∠A=50°,求∠ABO的度数;
(2)如图2,若点C在射线AE上,OB平分∠AOC交AE于点B,OD平分∠COP交AE于点D,∠ABO-∠AOB=70°,求∠ADO的度数;
(3)如图3,若∠A=α,依次作出∠AOP的角平分线OB,∠BOP的角平分线OB1,∠B1OP的角平分线OB2,…,∠Bn-1OP的角平分线OBn,其中点B,B1,B2,…,Bn-1,Bn都在射线AE上,试求∠ABnO的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,G为BC边上一点,BE⊥AG于E,DF⊥AG于F,连接DE.
(1)求证:△ABE≌△DAF;
(2)若AF=1,四边形ABED的面积为6,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形OABC是平行四边形,点C在x轴上,反比例函数y= ![]() (x>0)的图象经过点A(5,12),且与边BC交于点D.若AB=BD,则点D的坐标为 .
(x>0)的图象经过点A(5,12),且与边BC交于点D.若AB=BD,则点D的坐标为 . 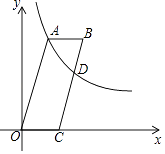
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com