
����Ŀ����֪����ͼ1������OP��AE����AOP�Ľ�ƽ���߽�����AE�ڵ�B��
��1������A=50�������ABO�Ķ�����
��2����ͼ2������C������AE�ϣ�OBƽ�֡�AOC��AE�ڵ�B��ODƽ�֡�COP��AE�ڵ�D����ABO-��AOB=70�������ADO�Ķ�����
��3����ͼ3������A=��������������AOP�Ľ�ƽ����OB����BOP�Ľ�ƽ����OB1����B1OP�Ľ�ƽ����OB2��������Bn-1OP�Ľ�ƽ����OBn�����е�B��B1��B2������Bn-1��Bn��������AE�ϣ������ABnO�Ķ�����

���𰸡���1��65������2��35������3����ABnO=![]() ��
��
��������
��1������ƽ���ߵ����ʵó���A=��1=50��������ƽ�ǵĶ�����á�AOP=130�������ݽ�ƽ���ߵ����ʺ�ƽ���ߵ�������á�ABO=��2=65����
��2����Ϊ��ABO=��ACO+��BOC����ABO-��AOB=70������BOC=��AOB����á�ACO=70��������ƽ���ߵ�������á�COP=��ACO=70��������������á�ADO=35����
��3�����ݣ�1����2���Ĺ��ɼ�����ã�
��1����ͼ1��
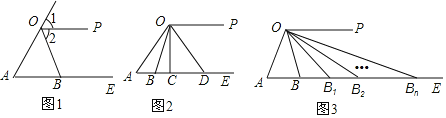
��OP��AE��
���A=��1=50����
���AOP=130����
�ߡ�2=��AOB��
���2=65����
���ABO=��2=65����
��2����ͼ2���ߡ�ABO=��ACO+��BOC����ABO-��AOB=70��
���ACO+��BOC-��AOB=70����
�ߡ�BOC=��AOB��
���ACO=70����
��OP��AE��
���COP=��ACO=70������POD=��ADO��
�ߡ�POD=��COD=![]() ��COP=35��
��COP=35��
���ADO=35����
��3����ͼ3���ɣ�1����֪����ABO=![]() ��180��-��������AB1O=
��180��-��������AB1O=![]() ��180��-��OBB1��=
��180��-��OBB1��=![]() ��ABO=
��ABO=![]() ��180��-��������AB2O=
��180��-��������AB2O=![]() ��180��-��������
��180��-��������
���ABnO=![]() ��
��


 ����ͬ�����Ծ�ϵ�д�
����ͬ�����Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѧУ��֪�����꼶ѧ�����ҹ������ġ�һ��һ·�����˽�̶ȣ������ȡ���־��꼶ѧ�������ʾ����飬�ʾ�����4��ѡ�ÿλ�������ѧ����ѡ��ֻѡһ���A���dz��˽⣮B���˽⣮C��֪��һ�㣮D����ȫ��֪����������Ľ����������������������ͳ��ͼ�����������ͳ��ͼ�е���Ϣ������������⣺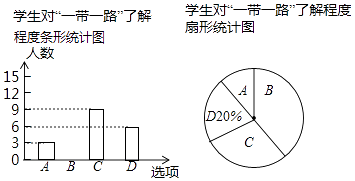
��1���ι������˶���ѧ����
��2����ȫ����ͳ��ͼ��
��3����У���꼶����600��ѧ����������ơ��˽⡱��ѧ��Լ�ж�������
��4���ڡ��dz��˽⡱��3���У���2��Ů����1����������ʦ�����3������ѡ����������Ա�������б�����״ͼ�������ѡ�е�����ǡ����һ����һŮ���ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ȤС��20λͬѧ��ʵ������еĵ÷�������±����������������ݵ���������λ�����������������ݵ�ƽ�����������˴β����÷ְ������Ƴ���ͼ��ʾ������ͳ��ͼ�����ٵ�Բ�ĽǶ����Ƕ��٣�
�÷֣��֣� | 10 | 9 | 8 | 7 |
�������ˣ� | 5 | 8 | 4 | 3 |
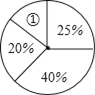
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪a��������2��2��3��b��|��9|+7��c��![]() ��
��
��1����3[a����b+c��]��2[b����a��2c��]��ֵ��
��2����A��![]() ����1��3��2��B��|a|��b+c���ԱȽ�A��B�Ĵ�С��
����1��3��2��B��|a|��b+c���ԱȽ�A��B�Ĵ�С��
��3����ͼ����֪��D���߶�AC���е㣬��B���߶�DC�ϵ�һ�㣬��CB��BD��2��3����AB��![]() cm����BC�ij���
cm����BC�ij���
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ֱ�����ǰ��ֱ�Ƕ���C������һ��
(1)����DCE��28��10'�����ACB�Ķ�����
(2)����ACB��148��21'�����DCE�Ķ�����
(3)ֱ��д����ACB���DCE��������ϵ��
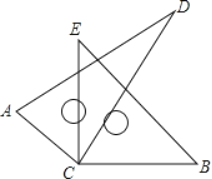
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ��ǿ��Ѵ������ij�ж�һ��ˮ�ӽ��мӹ̣���ͼ���ӹ�ǰ��ˮ�ӵĺ����������ABCD����֪ӭˮ����AB=12�ף���ˮ����CD=12 ![]() �ף���B=60�㣬�ӹ̺���ˮ�ӵĺ����Ϊ����ABED��tanE=
�ף���B=60�㣬�ӹ̺���ˮ�ӵĺ����Ϊ����ABED��tanE= ![]() ����CE�ij�Ϊ�ף�
����CE�ij�Ϊ�ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ѧУ��ʵ��¥������һ����ѧ¥��С����ʵ��¥�Ĵ���C��ý�ѧ¥����D������Ϊ18�㣬��ѧ¥�ײ�B�ĸ���Ϊ20�㣬����ʵ��¥���ѧ¥֮��ľ���AB=30m.
�������ȷ��0.1m���ο����ݣ�tan20���0.36,tan18���0.32��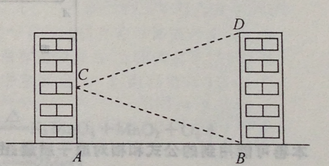
��1�����BCD�Ķ���.
��2�����ѧ¥�ĸ�BD
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������߸�����1����2����2����4����4����8����8����������ͼ1��3��Բ�����ཻ�ֳ�7�����֣��У�ʹ��ÿ��Բ�ڲ���4����֮����ȣ��������Ϊm����ͼ2������һ�������ʱm��64�������е���У�m�����ֵΪ_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijѧϰС�����о�����y= ![]() x3��2x��ͼ��������ʱ�����б�����㲢������ͼ���һ���֣�
x3��2x��ͼ��������ʱ�����б�����㲢������ͼ���һ���֣�
x | �� | ��4 | ��3.5 | ��3 | ��2 | ��1 | 0 | 1 | 2 | 3 | 3.5 | 4 | �� |
y | �� | �� | �� |
|
|
| 0 | �� | �� | �� |
|
| �� |
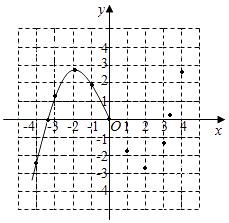
��1���벹ȫ����ͼ��
��2������ ![]() x3��2x=��2ʵ�����ĸ���Ϊ��
x3��2x=��2ʵ�����ĸ���Ϊ��
��3���۲�ͼ��д���ú������������ʣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com