
在Rt△ABC中,∠C=90°,∠A=60°,∠A,∠B,∠C的对边分别为a,b,c,a+b=3+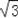
 ,请你根据此条件,求斜边c的长.
,请你根据此条件,求斜边c的长.

科目:初中数学 来源: 题型:
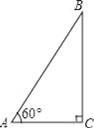
如图,关于∠α与∠β的同一种三角函数值,有三个结论:①tanα>tanβ,②sinα>sinβ,③cosα>cosβ.正确的结论为( )
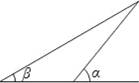

A.①② B.②③ C.①③ D.①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
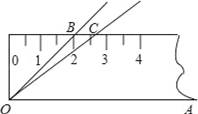
如图,将45°的∠AOB按下面的方式放置在一把刻度尺上:顶点O与尺下沿的端点重合,OA与尺下沿重合,OB与尺上沿的交点B在尺上的读数恰为2cm.若按相同的方式将37°的∠AOC放置在该刻度尺上,则OC与尺上沿的交点C在尺上的读数约为 cm.(结果精确到0.1cm,参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)

查看答案和解析>>
科目:初中数学 来源: 题型:
阅读下面材料:
小明遇到下面一个问题:如图1所示,AD是△ABC的角平分线,AB=m,AC=n,求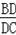
 的值.
的值.


小明发现,分别过B,C作直线AD的垂线,垂足分别为E,F.通过推理计算,可以解决问题(如图2).请回答,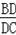
 = .
= .
参考小明思考问题的方法,解决问题:
如图3,四边形ABCD中,AB=2,BC=6,∠ABC=60°,BD平分∠ABC,CD⊥BD.AC与BD相交于点O.
(1)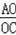
 = .
= .
(2)tan∠DCO= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com