
阅读下面材料:
小明遇到下面一个问题:如图1所示,AD是△ABC的角平分线,AB=m,AC=n,求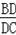
 的值.
的值.


小明发现,分别过B,C作直线AD的垂线,垂足分别为E,F.通过推理计算,可以解决问题(如图2).请回答,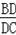
 = .
= .
参考小明思考问题的方法,解决问题:
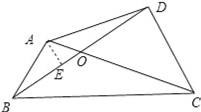
如图3,四边形ABCD中,AB=2,BC=6,∠ABC=60°,BD平分∠ABC,CD⊥BD.AC与BD相交于点O.
(1)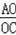
 = .
= .
(2)tan∠DCO= .
【考点】相似三角形的判定与性质.
【分析】小明的思路是先证明△BDF∽△CDE,得出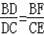
 ,再证明△ABF∽△ACE,得出
,再证明△ABF∽△ACE,得出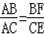
 ,因此得出
,因此得出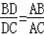
 .
.
(1)根据小明的结论得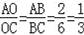
 ;
;
(2)作AE⊥BD于E,证明△AOE∽△COD,求出AE、BE、DE、OD、的长即可求出tan∠DCO的值.
【解答】解: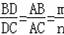
 ;
;
(1)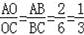
 ;
;
(2)作AE⊥BD于E,如图所示:
∵CD⊥BD,AE⊥BD,
∴AE∥CD,
∴△AOE∽△COD,
∴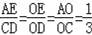
 ,
,
∵CD=3,∴AE=1,
∵BD平分∠ABC=60°,
∴∠ABD=∠DBC=30°,
∴BD=3
 ,
,
∵AB=2,
∴BE=
 ,
,
∴DE=2
 ,
,
∴OD=2
 ×
×
 =
=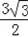
 ,
,
∴tan∠DCO=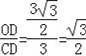
 .
.

【点评】本题考查了相似三角形的判定与性质以及锐角三角函数的运用;证明三角形相似是解决问题的关键.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:初中数学 来源: 题型:
如图,在△ABC,∠C=90°,∠B=15°,AB的中垂线DE交BC于D,E为垂足,若BD=10cm,则AC等于( )


A.10cm B.8cm C.5cm D.2.5cm
查看答案和解析>>
科目:初中数学 来源: 题型:
如图AB是半圆的直径,图1中,点C在半圆外;图2中,点C在半圆内,请仅用无刻度的直尺按要求画图.


(1)在图1中,画出△ABC的三条高的交点;
(2)在图2中,画出△ABC中AB边上的高.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com