如图AB是半圆的直径，图1中，点C在半圆外；图2中，点C在半圆内，请仅用无刻度的直尺按要求画图．
（1）在图1中，画出△ABC的三条高的交点；
（2）在图2中，画出△ABC中AB边上的高．
阅读快车系列答案科目：初中数学 来源： 题型：
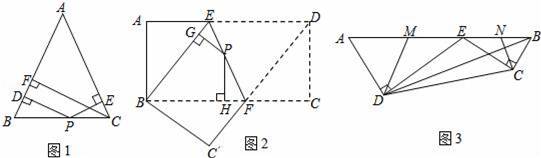
【问题情境】如图1，在△ABC中，AB=AC，点P为边BC上的任一点，过点P作PD⊥AB，PE⊥AC，垂足分别为D、E，过点C作CF⊥AB，垂足为F．求证：PD+PE=CF．
【结论运用】如图2，将矩形ABCD沿EF折叠，使点D落在点B上，点C落在点C′处，点P为折痕EF上的任一点，过点P作PG⊥BE、PH⊥BC，垂足分别为G、H，若AD=8，CF=3，求PG+PH的值；
【迁移拓展】图3是一个航模的截面示意图．在四边形ABCD中，E为AB边上的一点，
ED⊥AD，EC⊥CB，垂足分别为D、C，且AD•CE=DE•BC，AB=8，AD=3，BD=7；M、N分别为AE、BE的中点，连接DM、CN，求△DEM与△CEN的周长之和．
查看答案和解析>>
科目：初中数学 来源： 题型：
如图，关于∠α与∠β的同一种三角函数值，有三个结论：①tanα＞tanβ，②sinα＞sinβ，③cosα＞cosβ．正确的结论为（ ）
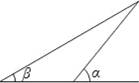
A．①② B．②③ C．①③ D．①②③
查看答案和解析>>
科目：初中数学 来源： 题型：
阅读下面材料：
小明遇到下面一个问题：如图1所示，AD是△ABC的角平分线，AB=m，AC=n，求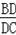
的值．
小明发现，分别过B，C作直线AD的垂线，垂足分别为E，F．通过推理计算，可以解决问题（如图2）．请回答，= ．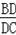
参考小明思考问题的方法，解决问题：
如图3，四边形ABCD中，AB=2，BC=6，∠ABC=60°，BD平分∠ABC，CD⊥BD．AC与BD相交于点O．
（1）
= ．
（2）tan∠DCO= ．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
）÷
，再从﹣2≤a≤2中选一个你认为合适的整数作为a的值代入求值．
﹣1|﹣（
）﹣2﹣2sin60° 
m，圆心角为120°，则此扇形的弧长是 cm．