
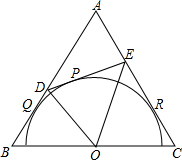
 如图,在边长为a的等边△ABC中,半圆O的直径在BC上,又分别与AB、AC相切于点Q、R,点P是弧QR上(不包括Q、R点)任意一点,过点P的切线分别与AB、AC相交于点D、E.
如图,在边长为a的等边△ABC中,半圆O的直径在BC上,又分别与AB、AC相切于点Q、R,点P是弧QR上(不包括Q、R点)任意一点,过点P的切线分别与AB、AC相交于点D、E.分析 (1)连结OQ、OR,如图,根据切线的性质得OQ⊥AB,OR⊥AC,OQ=OR,再利用等边三角形的性质得∠B=∠C=60°,则根据“AAS”可判断△OBQ≌△OBR,于是得到OB=OC;
(2)OB=OC=$\frac{1}{2}$BC=$\frac{1}{2}$a,在Rt△OBQ中利用含30度的直角三角形三边的关系得BQ=$\frac{1}{2}$OB=$\frac{1}{4}$a,则CR=BQ=$\frac{1}{4}$a,再根据切线的性质和切线长定理得OP⊥DE,DQ=DP,EP=ER,则利用等线段代换可得△ADE的周长=AD+AE+DE=AQ+AR=$\frac{3}{2}$a;由于DQ⊥OQ,DP⊥OP,DQ=DP,则根据角平分线定理的逆定理得∠1=∠2,同理可得∠3=∠4,所以∠DOE=$\frac{1}{2}$∠QOR,然后利用四边形内角和得∠QOR=180°-∠A=120°,则∠DOE=60°;
(3)由于∠1=60°-∠4,则∠QDO=90°-∠1=30°+∠4,而∠COE=∠COR+∠4=30°+∠4,则∠BDO=∠COE,于是可证明△OBD∽△ECO,利用相似比可得BD•CE=OB•OC=$\frac{1}{4}$a2,接着利用等线段代换可得BD+CE=BQ+DE+CR=$\frac{\sqrt{5}}{2}$a,然后利用完全平方公式可计算出BD2+CE2的值.
解答 (1)证明:连结OQ、OR,如图,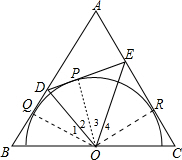 ∵半圆O的直径在BC上,分别与AB、AC相切于点Q、R,
∵半圆O的直径在BC上,分别与AB、AC相切于点Q、R,
∴OQ⊥AB,OR⊥AC,OQ=OR,
∵△ABC为边长为a的等边三角形,
∴∠B=∠C=60°,
在△OBQ和△OBR中,
$\left\{\begin{array}{l}{∠B=∠C}\\{∠BQO=∠CRO}\\{OQ=OR}\end{array}\right.$,
∴△OBQ≌△OBR,
∴OB=OC;
(2)解:OB=OC=$\frac{1}{2}$BC=$\frac{1}{2}$a,
在Rt△OBQ中,∵∠B=60°,
∴BQ=$\frac{1}{2}$OB=$\frac{1}{4}$a,
∴CR=BQ=$\frac{1}{4}$a,
∵过点P的切线分别与AB、AC相交于点D、E,
∴OP⊥DE,DQ=DP,EP=ER,
∴△ADE的周长=AD+AE+DE=AD+AE+DP+EP=AD+DQ+AE+ER=AQ+AR=a-$\frac{1}{4}$a+a-$\frac{1}{4}$a=$\frac{3}{2}$a;
∵DQ⊥OQ,DP⊥OP,DQ=DP,
∴∠1=∠2,
同理可得∠3=∠4,
∴∠DOE=$\frac{1}{2}$∠QOR,
∵∠QOR=180°-∠A=180°-60°=120°,
∴∠DOE=60°;
(3)解:∵∠1+∠4=60°,
∴∠1=60°-∠4,
∴∠QDO=90°-∠1=90°-(60°-∠4)=30°+∠4,
而∠COE=∠COR+∠4=30°+∠4,
∴∠BDO=∠COE,
而∠B=∠C,
∴△OBD∽△ECO,
∴$\frac{BD}{OC}$=$\frac{OB}{CE}$,
∴BD•CE=OB•OC=$\frac{1}{4}$a2,
∵BD+CE=BQ+DQ+CR+ER=BQ+DP+EP+CR=BQ+DE+CR=$\frac{1}{4}$a+$\frac{\sqrt{5}-1}{2}$a+$\frac{1}{4}$a=$\frac{\sqrt{5}}{2}$a,
∴BD2+CE2=(BD+CE)2-2BD•CE=($\frac{\sqrt{5}}{2}$a)2-2×$\frac{1}{4}$a2=$\frac{3}{4}$a2.
点评 本题考查了圆的综合题:熟练掌握切线的判定与性质、切线长定理和等边三角形的性质;灵活运用相似三角形的判定与性质进行几何计算.


 全能闯关100分系列答案
全能闯关100分系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
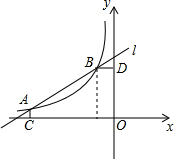 已知关于x的方程x2+2kx+k2-2k+1=0的两个实数根x1,x2满足x12=4-x22,反比例函数y=-$\frac{2k}{x}$的图象与直线l关于A(-4,m),B(-1,n)两点(如图),AC⊥x轴于C,BD⊥y轴于D.
已知关于x的方程x2+2kx+k2-2k+1=0的两个实数根x1,x2满足x12=4-x22,反比例函数y=-$\frac{2k}{x}$的图象与直线l关于A(-4,m),B(-1,n)两点(如图),AC⊥x轴于C,BD⊥y轴于D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
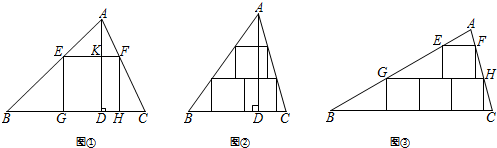
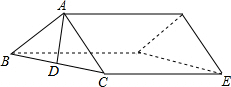 在我国南方农村,常见到如图的屋顶,为防雨需在房顶铺上油毡,已知AB=AC,AD为△ABC的中线,且AD=3m,BC=8m,CE=10m,问需要用油毡多少平方米?
在我国南方农村,常见到如图的屋顶,为防雨需在房顶铺上油毡,已知AB=AC,AD为△ABC的中线,且AD=3m,BC=8m,CE=10m,问需要用油毡多少平方米?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com