
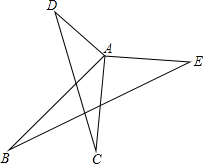
 如图,已知AD⊥AB,AC⊥AE,且AD=AB,AC=AE,请判断BE和CD的关系并证明.
如图,已知AD⊥AB,AC⊥AE,且AD=AB,AC=AE,请判断BE和CD的关系并证明. 分析 BE=CD,BE⊥CD,求出∠DAC=∠BAE,证△DAC≌△BAE,根据全等三角形的性质推出即可.
解答 解:BE=CD,BE⊥CD,
理由如下:
∵AD⊥AB,AE⊥AC,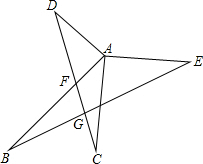
∴∠BAD=∠CAE=90°,
∴∠BAD+∠BAC=∠CAE+∠BAC,
即∠BAE=∠DAC,
在△DAC和△BAE中,
$\left\{\begin{array}{l}{AD=AB}\\{∠DAC=∠BAE}\\{AC=AE}\end{array}\right.$,
∴△ADC≌△ABE,
∴∠D=∠B,CD=BE,
∵∠D+∠AFD=90°,∠AFD=∠BFG,
∴∠ABG+∠BFG=90°,
∴∠BGF=90°,
∴∠DGE=90°,
∴BE⊥CD.
点评 本题考查了全等三角形的性质和判定的应用,注意:①全等三角形的判定定理有SAS,ASA,AAS,SSS,②全等三角形的性质是:全等三角形的对应边相等,对应角相等.


 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:初中数学 来源: 题型:解答题
 如图,已知直线l与⊙O相离.OA⊥l于点A,交⊙O于点P,OA=5,AB与⊙O相切于点B,BP的延长线交直线l于点C.
如图,已知直线l与⊙O相离.OA⊥l于点A,交⊙O于点P,OA=5,AB与⊙O相切于点B,BP的延长线交直线l于点C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
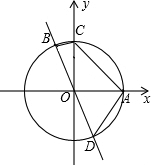 如图,已知⊙O经过点A(2,0)、C(0,2).直线y=kx(k≠0)与⊙O分别交于点B、D,则四点A、B、C、D组成的四边形面积的最大值为4$\sqrt{2}$.
如图,已知⊙O经过点A(2,0)、C(0,2).直线y=kx(k≠0)与⊙O分别交于点B、D,则四点A、B、C、D组成的四边形面积的最大值为4$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
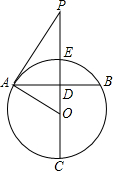 如图,过圆心O的直线PC垂直弦AB于点D,并且与⊙O交于C、E两点.
如图,过圆心O的直线PC垂直弦AB于点D,并且与⊙O交于C、E两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
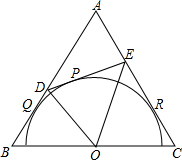 如图,在边长为a的等边△ABC中,半圆O的直径在BC上,又分别与AB、AC相切于点Q、R,点P是弧QR上(不包括Q、R点)任意一点,过点P的切线分别与AB、AC相交于点D、E.
如图,在边长为a的等边△ABC中,半圆O的直径在BC上,又分别与AB、AC相切于点Q、R,点P是弧QR上(不包括Q、R点)任意一点,过点P的切线分别与AB、AC相交于点D、E.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
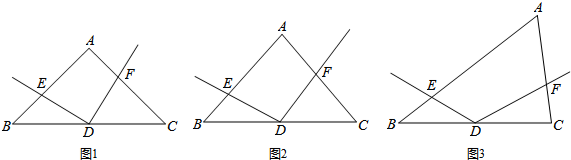
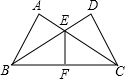 如图,∠A=∠D=90°,AB=DC,AC与BD相交于点E,F是BC的中点.下列说法:①BE=EC;②BF=FC;③EF⊥BC;④∠BEF=∠CEF,正确的有( )个.
如图,∠A=∠D=90°,AB=DC,AC与BD相交于点E,F是BC的中点.下列说法:①BE=EC;②BF=FC;③EF⊥BC;④∠BEF=∠CEF,正确的有( )个.| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 端午节小明来到奥体中心观看中超联赛第14轮重庆力帆主场迎战广州富力的比赛.进场时,发现门票还在家里,此时离比赛开始还有25分钟,于是立即步行回家取票,同时,他爸爸从家里吃饭骑自行车以小明3倍的速度给小明送票,两人在途中相遇,相遇后爸爸立即骑自行车吧小明送回奥体中心.如图,线段AB、OB分别表示父子俩送票、取票过程中,离奥体中心的距离S(米)与所用时间t(分钟)之间关系的图象,结合图象解答下列问题(假设骑自行车和步行的速度始终保持不变):
端午节小明来到奥体中心观看中超联赛第14轮重庆力帆主场迎战广州富力的比赛.进场时,发现门票还在家里,此时离比赛开始还有25分钟,于是立即步行回家取票,同时,他爸爸从家里吃饭骑自行车以小明3倍的速度给小明送票,两人在途中相遇,相遇后爸爸立即骑自行车吧小明送回奥体中心.如图,线段AB、OB分别表示父子俩送票、取票过程中,离奥体中心的距离S(米)与所用时间t(分钟)之间关系的图象,结合图象解答下列问题(假设骑自行车和步行的速度始终保持不变):查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com