
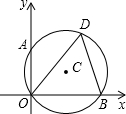
 如图,⊙C经过原点且与两坐标轴分别交于点A和点B,点A的坐标为(0,2),D为⊙C在第一象限内的一点且∠ODB=60°,解答下列各题:
如图,⊙C经过原点且与两坐标轴分别交于点A和点B,点A的坐标为(0,2),D为⊙C在第一象限内的一点且∠ODB=60°,解答下列各题:分析 (1)在Rt△OAB中,只要证明∠OAB=∠ODB=60°,利用直角三角形30度角性质即可解决问题.
(2)过C点作CE⊥OA于E,CF⊥OB于F.利用勾股定理求出OB的长,再利用垂径定理以及三角形中位线定理求出CE、CF即可解决问题.
(3)作DH⊥OB于H,连结CD,所以当D、C、F三点在同一直线上时,DH最大为3.此时△OBD的面积也最大,由此即可即可解决问题.
解答 解:(1)连接AB.
∵∠ODB=∠OAB,∠ODB=60°
∴∠OAB=60°,
∵∠AOB是直角,
∴AB是⊙C的直径,
∴∠OBA=30°,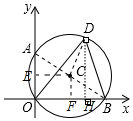
∴AB=2OA=4,
∴⊙C的半径r=2;
(2)过C点作CE⊥OA于E,CF⊥OB于F,
在Rt△OAB中,由勾股定理得:OB2+OA2=AB2,
∴OB=2$\sqrt{3}$,
∴B的坐标为:(2$\sqrt{3}$,0)
由垂径定理得:OE=AE=1,OF=BF=$\sqrt{3}$,
∵AE=EO,AC=CB,
∴EC=$\frac{1}{2}$OB=$\sqrt{3}$,CF=$\frac{1}{2}$OA=1,
∴C的坐标为($\sqrt{3}$,1).
(3)作DH⊥OB于H,连结CD,
△OBD的面积=$\frac{1}{2}$OB•DH
因为DH≤CD+CF
所以当D、C、F三点在同一直线上时,DH最大为3.
此时△OBD的面积也最大,
∴点D的坐标为($\sqrt{3}$,$\sqrt{3}$).
点评 本题考查圆综合题、垂径定理、圆周角定理、坐标与图象的性质、三角形中位线定理、三角形的面积、垂线段最短等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,学会利用垂线段最短解决最值问题,属于中考压轴题.


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
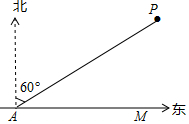 如图,在一计划修建的东西走向的铁路AM旁有一自然保护区P,在距该自然保护区中心P的15$\sqrt{2}$ km圆形区域内属于保护区范围,线路勘察队在距保护区中心P的30km的A处测得保护区中心P位于A的北偏东60°方向,若不改变铁路的原修建线路,铁路是否会破坏该保护区的保护区域?请通过计算加以说明.如果会破坏,铁路自A处开始至少沿东偏南多少度改线,才不会破坏该保护区的保护区域?
如图,在一计划修建的东西走向的铁路AM旁有一自然保护区P,在距该自然保护区中心P的15$\sqrt{2}$ km圆形区域内属于保护区范围,线路勘察队在距保护区中心P的30km的A处测得保护区中心P位于A的北偏东60°方向,若不改变铁路的原修建线路,铁路是否会破坏该保护区的保护区域?请通过计算加以说明.如果会破坏,铁路自A处开始至少沿东偏南多少度改线,才不会破坏该保护区的保护区域?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
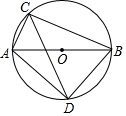 如图,AB是⊙O的直径,弦BC长为$4\sqrt{2}$,弦AC长为2,∠ACB的平分线交⊙O于点D.
如图,AB是⊙O的直径,弦BC长为$4\sqrt{2}$,弦AC长为2,∠ACB的平分线交⊙O于点D.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -1 | B. | +$\frac{1}{2}$ | C. | +$\frac{1}{3}$ | D. | -$\frac{1}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com